



Next: References
Up: Applications/New Directions
Previous: Distance Problems
We present some open questions related to the fixed point property
in the
following.
Some are more precise formulations of problem 1.1
for special cases, others are intended to put methods developed for
use with the fixed point property
to use in other areas.
-
For what classes of ordered sets does Xia's reduction algorithm
decide if an ordered set has a fixed point property?
I.e.,
(cf. Theorem 2.22)
for what classes of ordered sets does termination of Xia's
reduction algorithm with a non-empty graph imply
the existence of a fixed point free order-preserving map?
-
What is the average case complexity of problem 2.3.
(For average case complexity cf. [130].)
-
Is it possible to decide in polynomial time whether a given ordered
set is (connectedly) collapsible? Does Xia's algorithm terminate with
a graph with no edges when applied to a connectedly collapsible
ordered set? (There is an algorithm that decides
connected collapsibility in
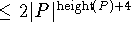 comparability checks, cf. [122].)
comparability checks, cf. [122].) -
Is there an infinitary analogue of connected collapsibility, which
again implies that all fixed point sets are connected?
This might also be a first step towards an analogue of acyclicity for
infinite ordered sets/graphs/simplicial complexes.
-
Is it possible to decide in polynomial time whether a given ordered
set is acyclic?
-
Is the problem whether a given truncated lattice has
a fixed point free order-preserving self-map NP-complete?
(Section 4.8 seems to indicate that the
problem is quite complex.)
-
The next problems have the same purposely vague formulations
as Problem 1.1 to allow for a wide variety of possible
approaches. (Naturally we can also ask the complexity question.)
-
(compare with [30], problem on p.233)
Characterize all (finite) ordered sets P such that
each order-preserving map
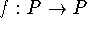 has a connected nonempty
set of fixed points.
has a connected nonempty
set of fixed points. -
Characterize all (finite) graphs that have the
fixed clique property.
(Some theorems are presented in [10] and in [120].
More questions on fixed cliques appear in [121].)
-
Characterize all (finite) simplicial complexes that have the
fixed simplex property.
(Some theorems are presented in [120].)
-
Characterize those ordered sets without infinite chains that have the
relational fixed point property (cf. section 3.5).
-
Let P,Q,R be finite ordered sets and assume Q is dismantlable.
Does the fact that
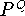 is isomorphic to
is isomorphic to
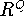 imply that P is isomorphic to R?
Can we use other families of retractions to
arrive at results similar to Proposition 5.5?
imply that P is isomorphic to R?
Can we use other families of retractions to
arrive at results similar to Proposition 5.5? -
Find a nondismantlable finite ordered set P such that
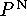 (where
(where 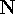 carries the discrete order)
has the fixed point property. This is a natural generalization of the
product problem which was solved in [104] for finite ordered sets.
It is easy to see that if P is finite and dismantlable, then
carries the discrete order)
has the fixed point property. This is a natural generalization of the
product problem which was solved in [104] for finite ordered sets.
It is easy to see that if P is finite and dismantlable, then
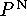 also is dismantlable. However there are no results
for infinite powers of non-dismantlable finite ordered sets.
A possible first candidate would be the set P1 in [110]
(which first appeared in [95]). It is connectedly collapsible,
which
might allow for arguments along the lines of [112].
The fact that we have infinitely many factors adds a large degree of
difficulty however.
also is dismantlable. However there are no results
for infinite powers of non-dismantlable finite ordered sets.
A possible first candidate would be the set P1 in [110]
(which first appeared in [95]). It is connectedly collapsible,
which
might allow for arguments along the lines of [112].
The fact that we have infinitely many factors adds a large degree of
difficulty however. -
Are there good estimates on how many order-preserving self maps of an
ordered set, i.e., what fraction of
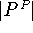 , must have a fixed point (cf. [103])?
, must have a fixed point (cf. [103])? -
Are the sets of fixed points of self maps of Z-acyclic
ordered sets always
connected? (For Q-acyclic ordered sets the answer is negative as
example 2.2 in [7] shows.)
-
What graph theoretical analogues are there of the Li-Milner theorem?
-
Is the
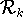 -core of an infinite set unique if it exists?
Is the
-core of an infinite set unique if it exists?
Is the 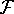 -core of an infinite set unique if it exists?
(Clearly there are nontrivial
-core of an infinite set unique if it exists?
(Clearly there are nontrivial 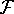 -cores: The rational
numbers with the natural order are an
-cores: The rational
numbers with the natural order are an 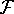 -core.)
Is the core in the sense of Li and Milner unique if it exists
(cf. Question 1 in [70], p.353)?
-core.)
Is the core in the sense of Li and Milner unique if it exists
(cf. Question 1 in [70], p.353)? -
Is it possible to prove uniqueness results for ``cores with respect to
dismantlability via escamotable points" similar to Theorem
3.14?
-
Is it possible to prove analytical results that use the conditional
completeness of the
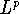 -spaces resp. the lattice structure of
spaces of continuous functions?
(E.g. to obtain a starting point
-spaces resp. the lattice structure of
spaces of continuous functions?
(E.g. to obtain a starting point 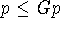 one could look for a
function f such that
one could look for a
function f such that 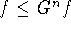 and use the supremum
of
and use the supremum
of 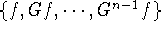 as p.
This idea is exhibited in [133], Corollary 2.)
as p.
This idea is exhibited in [133], Corollary 2.) -
(This question is due to B. Larose, [69]
and is mentioned also at the
end of [132]. Common fixed points were for example
also considered on topological
spaces for continuous maps in [25], resp. for families of
commuting order-preserving maps in [133].)
Under what conditions on the ordered set P do all automorphisms
of P have a common fixed point?
Is the fixed point property or any of the many sufficient conditions
for the fixed point property also sufficient for this
property?
Acknowledgements (this mathematician's apology):
Much of this survey stems from preprints that were made available
to me by various researchers and from private communications.
Among the individuals that I wish to thank
are
K. Baclawski (for a preprint of [6]),
D. Duffus (for informing me about the work of Goddard and Williamson
and a preprint of [29]),
J.D. Farley (for the argument after the introduction of Lefschetz numbers,
a copy of [40]
and for pointing out [48]),
T. Goddard (for letting me use proof 1 of Theorem 2.14),
S. Hazan (for a copy of [48] and an early version of [10]),
S. Heikkilä (for a large number of reprints on nonlinear analysis),
S. Homer (for a preprint of [65]),
T. McKee and E. Prisner (for a preprint of [80] and the permission to
include a translation to Z-homology),
I. Rival (for the invitation to write this,
patience as I was writing it and much general encouragement),
M. Roddy (for the very inspiring collaboration on finding an example
of an ordered set with the fixed point property for which
Xia leaves some edges),
A. Rutkowski (for a preprint of [44] and delightful collaboration
on [113]),
G. Sabidussi (for references on the fixed clique property and the
final coordinates of [10]),
R. Stanley (for pointing out [41] and [59]),
J. Wang (for a preprint of [130]),
plus an unknown referee (for the argument on triangulations of  ),
but most of all my wife and children
(for continuing to put up with me).
The strong influence of very recent results shows how fertile this
field and its connections to
analysis, algebraic topology,
complexity theory, graph theory are
(in fact the paper [120]
as well as the notion of connected collapsibility materialized
during the writing of this manuscript).
The style of presentation definitely is my own as I frequently
changed the original presentation to fit the most difficult
of conditions: It had to be simple enough so even I could understand it.
The algebraic topology chapter is definitely too brief and
too dense, yet I hope it will do for other researchers
who currently don't use algebraic topology the same that it did
for me: Provide a start into using this powerful theory.
Likewise the section on applications to analysis is too short, but I
hope that the mentioning of this body of work will
direct more attention in this direction.
(As seen in question 15 my ideas in this direction are quite
trivial and possibly impractical so far.)
I apologize for any over-simplifications, missing references
and unclear spots
that may remain and I hope that any remaining errors
in the manuscript are
not mathematically significant.
),
but most of all my wife and children
(for continuing to put up with me).
The strong influence of very recent results shows how fertile this
field and its connections to
analysis, algebraic topology,
complexity theory, graph theory are
(in fact the paper [120]
as well as the notion of connected collapsibility materialized
during the writing of this manuscript).
The style of presentation definitely is my own as I frequently
changed the original presentation to fit the most difficult
of conditions: It had to be simple enough so even I could understand it.
The algebraic topology chapter is definitely too brief and
too dense, yet I hope it will do for other researchers
who currently don't use algebraic topology the same that it did
for me: Provide a start into using this powerful theory.
Likewise the section on applications to analysis is too short, but I
hope that the mentioning of this body of work will
direct more attention in this direction.
(As seen in question 15 my ideas in this direction are quite
trivial and possibly impractical so far.)
I apologize for any over-simplifications, missing references
and unclear spots
that may remain and I hope that any remaining errors
in the manuscript are
not mathematically significant.




Next: References
Up: Applications/New Directions
Previous: Distance Problems
Bernd.S.W.Schroder
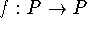 has a connected nonempty
set of fixed points.
has a connected nonempty
set of fixed points.