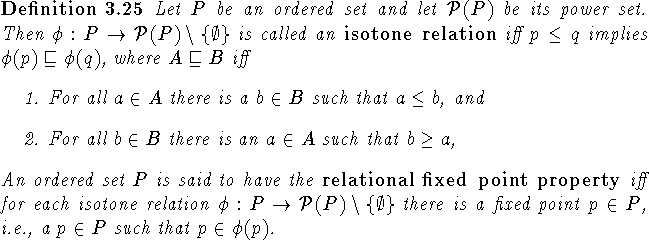
Isotone relations are a beautiful variation on the order-preserving mapping theme that has a nice solution to its analogue of Problem 1.1 in the finite case. Most results in this section are due to or inspired by Walker (cf. [129]). For more on the relational fixed point property consider [46], [64], [75], [107].
Clearly the relational fixed point property implies the
fixed point property and it is also preserved by retractions.
Unfortunately as pointed out in
[46], p.28, (2) or
[75], bottom of p.161,
the set 
with its natural order does not have the
relational fixed point property.
Thus the restriction to ordered sets with no infinite chains is only
natural.
In ordered sets with no infinite chains it is then easy to prove
(cf. [129], Proposition 5.2) that
if 
is an isotone relation and there are 
such that
and 
, then 
has a fixed point.
This allows us to reflect the relational fixed point property:
Since (cf. [129], Theorem 5.6) an ordered set P with no infinite chains, the relational fixed point property and more than one point must have an irreducible point we arrive at the conclusion that the situation described above might be the only case that occurs. To back this conjecture we present:
Proof:
By the main result in [70], the 
-core
of P exists and by Theorem 5.6 in [129] it has the
relational fixed point
property iff it is a singleton. \
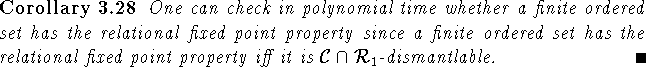
We can also use these results to obtain a quick proof of the finite case of Fofanova and Rutkowski's result on ordered sets of width 2 (recall that the width of an ordered set P is the size of the largest antichain in P, where an antichain is a subset of pairwise noncomparable elements):
Proof:
We will show that P has the fixed point property iff P has the
relational fixed point property, which by Theorem 3.27
implies the result.
It is clear that the relational fixed point property implies the
fixed point property. Now suppose P does not have the relational
fixed point property. Let
be an isotone relation with no fixed point.
Since P has width 2, 
is a chain for each 
.
Now 
is a fixed point free
order-preserving map. \
