The problem of deciding whether a finite ordered set has a fixed point free automorphism was found by Williamson to be NP-complete (cf. [132], Fact 5.1 or Theorem 2.14 here), i.e.,
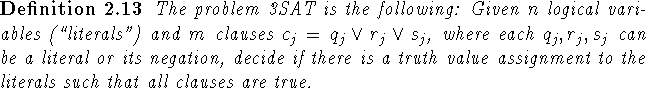
We will present two proofs of this theorem here. One by Goddard that reduces the problem to a known NP-complete problem, namely the determination if a given graph has a fixed point free automorphism (cf. [79]). The other is Williamson's original adaptation of Lubiw's proof in [79], which reduces the problem to 3SAT. This proof will be sketched only. For the first proof we need:
Proof 1 of Theorem 2.14:
(T. Goddard, private communication, also cf. [29])
By [79] it is NP-complete to decide if a given graph has a
fixed point free automorphism. We will show that any
algorithm that decides if an
arbitrary
ordered set P has a fixed point free automorphism in
q(|P|) steps
also decides
if an arbitrary graph G=(V,E)
has a fixed point free automorphism
in q'(|V|) steps,
where q,q' are polynomials.
Let G=(V,E) be a graph. Order the set
via the order 
defined as follows:
is reflexive,
are related,
and 
, then
v<(e,x) iff 
.
is a fixed point free automorphism, then
is a fixed point free automorphism of G.
Conversely, if 
is a fixed point free automorphism
of G, then
let
and
f is a fixed point free automorphism of P. \
Thus we even know that the problem to decide if an ordered set of height 1 has a fixed point free automorphism is NP-complete (this is also noted as Fact 5.2 in [132]). This is interesting in the light of Theorem 3.21 and Corollary 3.24, which show that there is an efficient algorithm to detect if an ordered set of height 1 has a fixed point free order-preserving self map. Our second proof is a reduction to 3SAT itself.
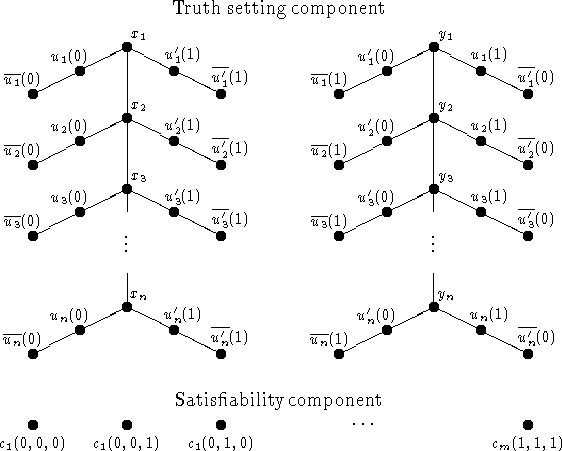
Figure 2: The ordered set used in the second proof of Theorem
2.14:
Consider an instance of 3SAT with m distinct clauses
, each of which contains
exactly 3 distinct literals 
out of 
.
The satisfiabiliy component is an antichain of points
, where abc counts from zero to 7 in binary.
The truth setting component has comparabilities as indicated.
Finally (not indicated in the figure)
the upper covers of are
and 
.
Proof 2 of Theorem 2.14:
(cf. [132], Fact 5.1; we present a sketch)
For a given instance C of 3SAT which we can without loss of generality
choose to have m distinct clauses
each of which has 3 distinct literals
out of
we construct the ordered set P as indicated in Figure 2.
Note that each has a unique set of 6 upper covers.
For 
, let
.
Then it is easy to see that every automorphism
of P must fix the satisfiability component and every 
.
Each has exactly four fixed point free automorphisms, of which only
and
(we remain consistent with the notation in [132] here)
can possibly extend to an automorphism of P
(the other two map sets that have a lower bound in the satisfiability
component to sets that do not have lower bounds).
To show that P has a fixed point free automorphism iff
there is a satisfying assignment for C first assume that
is a fixed point free automorphism.
If 
, set 
TRUE. Otherwise
we have
, and we set FALSE.
Now if 
and 
were all false for some j, then
the definitions of 
and 
indicate
that 
must interchange 
and 
,
and 
, and
and 
.
Since these are the upper covers of 
we conclude that
is a fixed point of , a contradiction.
On the other hand if 
is a
satisfying assignment for C (with 0 standing for FALSE and
1 standing for TRUE as usual), we define as follows:
Set 
if is true (1),
set 
if is false (0) and
set
,
where 
denotes addition modulo 2.
Since one of is 1 (true),
has no fixed points.
trivially is an automorphism on the truth setting component.
Since addition of a 1 or a 0 modulo 2 is injective, is
injective and hence bijective on the satisfiability component.
Finally one checks that is order-preserving. \
Using the characterization in Remark 2.11 we can also record some known results as easy consequences:
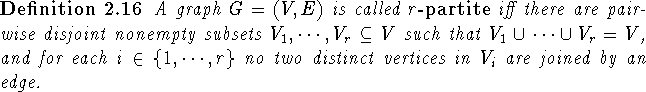
Proof:
If there was an algorithm that decides
if a given r-partite
graph G=(V,E) with partition 
and 
contains an r-clique
in q(|V|) steps, then by
Remark 2.11
there would be
an
algorithm that determines if the
fixed point free automorphism graph of a
given ordered set P has a
|P|-clique in q'(|P|) steps.
Thus we could determine if
a given ordered set P has a fixed point free automorphism in
q''(|P|) steps (q,q',q'' all polynomials).\
Proof:
If there was an algorithm that determines
if a given graph
G=(V,E) with 
has an r-clique
in q(|V|) steps, then
this algorithm would
decide if a given r-partite
graph G=(V,E) with partition
and
has an r-clique
in q(|V|) steps. \
