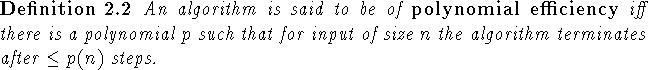
Obviously answering the question ``Does P have the fixed point property?"
for arbitrary P is a hard problem as one would need to check every
order-preserving map 
for a fixed point.
Since every ordered set P has at least
order-preserving self maps
(cf. [35]) this approach
obviously is exponentially hard.
(In fact computational data such as presented for example in
[86] indicates that ordered sets should
have many more order-preserving
self-maps than this lower bound indicates.)
Thus we formally have to reformulate the problem to:
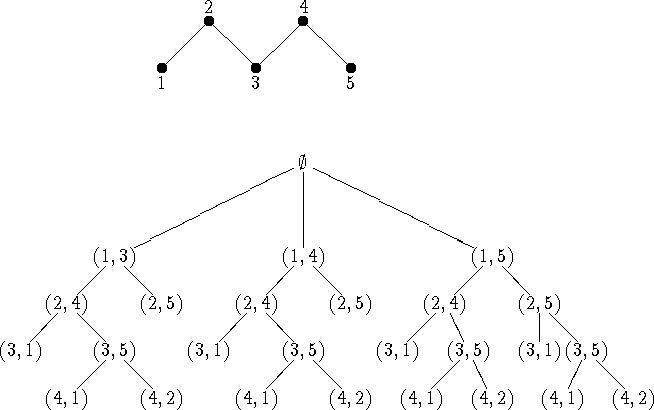
Figure 1: The depth-first search tree in searching for a fixed point
free order-preserving map of a five element fence.
This can be viewed as the NP (cf. Definition 2.12)
version of the fixed point problem.
Let us first consider the most simple-minded approach to
the problem.
(This approach
for a reduced tree
is described in the second half of [134].
Similar programs were used
on the whole tree
to count order-preserving mappings in
[86].)
This will lead us to a very nice algorithm by Xia and some results
that show the similarity between the problem of finding a fixed point free
map and finding a fixed point free automorphism.
For the actual proof of the NP-completeness of problem 2.3
the reader is referred to [29].
First one realizes that for a fixed point free order-preserving map
on a finite ordered set P
we must have 
for all 
.
(Otherwise, say, 
implies
and this iteration process
must reach a fixed point in finitely many steps.)
Now number the points of P from 1 to |P|.
For every point k let the set
be
ordered by the natural order of the second component.
Attempting to construct a fixed point free order-preserving map
we can construct fixed point free order-preserving partial maps.
We start with 
and add the first ordered pair
in 
to assign an image
to 1. Then we add the first ordered pair
in 
to assign an image to 2.
We continue until the partial map thus obtained is no longer
order-preserving. Then we remove the last added ordered pair
and
add instead the next ordered pair out of
. If there is no such pair, we
remove the ordered pair
(in 
)
that was added second-to-last and continue
as indicated (i.e., add the next pair in
or remove the pair in 
that was last added).
In this fashion we will find a fixed point free
order-preserving map if there is one. The search tree for a simple
example (a five element fence) is indicated in Figure 1.
As one can see there is a lot of duplication in the tree.
For example,
in every branch it is the incompatibility of (3,1) with
(2,4) which causes the first incident of ``backtracking".
One might be able to save time if one could detect and use such
incompatibilities earlier.
This seems to be the idea of Xia's algorithm
(cf. [134], resp. section 2.4, readers
exclusively interested in
Xia's algorithm can skip section 2.3).
We present these ideas in the following, choosing the language of
graph theory rather than the language of formal
concept analysis.
