In this section we briefly indicate how to construct a large family of examples of finite ordered sets that have a fixed point free automorphism and are such that all retracts have the fixed point property. This shows that despite some nice results for special classes of ordered sets the approach 3 in the introduction might not lead to a resolution of the fixed point problem, as there are too many forbidden retracts. Theorem 4.51 was revealed to the author by an anonymous referee. It also gives a negative answer to Problem 2 in [96]. The author would like to hereby express his gratitude to this referee.
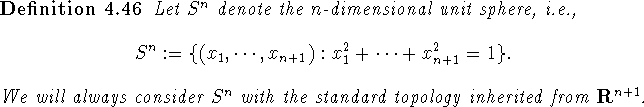
Proof:
Let 
be a retraction, i.e., a continuous
idempotent map with 
.
Then 
is isomorphic to a
retract of the n-dimensional unit ball which has the
topological fixed point property by Brouwer's fixed point theorem.
\
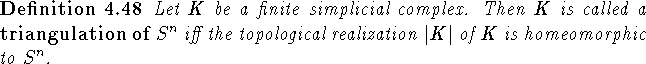
Proof:
Let 
be the
truncated incidence lattice of the triangulation
K of .
Let 
be a nontrivial
retraction
with 
.
Then there is a minimal element m of
that is not in 
:
Indeed otherwise r fixes all minimal elements of , which
implies 
for all 
. Then there is a
such that r(y)>y and r(p)=p for all 
.
Then y has exactly one upper cover and
there is a maximal element 
such that
has exactly one point (otherwise y has more than
one upper cover).
Thus M is the only upper bound of y.
But then every point x that is in the interior of the
topological realization 
of y is such that
for all 
small enough we have that
is homeomorphic to
the upper half space
.
Since is an n-dimensional manifold
without boundary this is a contradiction
to |K| being homeomorphic to .
Let 
be an order-preserving map.
Let 
. For each minimal
element
choose a minimal element 
such that
.
For 
not minimal let
Then G is order-preserving on .
Moreover 
is a retraction
and induces a
simplicial map on K that is a
nontrivial
retraction
(we have shown above that the retract does not contain all minimal
elements), which can be
extended to a continuous retraction 
.
Now by Lemma 4.47 
has the topological
fixed point property.
Thus the continuous map on R[|K|] induced by G has a fixed point p.
Let S be the smallest simplex in 
such that 
.
Then G maps S to a sub-simplex of S, i.e.,
and thus G has a fixed point.
Thus 
has a fixed point, which must be a fixed point
of f.
\
Proof:
For each simplex S of K let A(S):=-S.
By hypothesis this is well-defined.
Since no simplex is equal to its antipode
is a fixed point free
order-preserving automorphism of .
By Lemma 4.50 all nontrivial retracts of
have the (order-theoretical) fixed point property.
\
