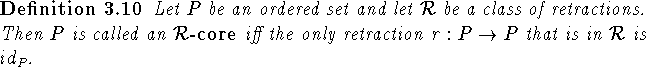
Having such a dismantling process available it is reasonable to ask when it might stop (compare with the removal step for Xia's reduction algorithm and Proposition 2.21). The problems encountered at the limit ordinal are quite subtle (for example in their worst form encountered when trying to infinite-dismantle the one-way infinite fence) and are dealt with in [70]-[74], [76] and [77], where conditions on the ordered set are given that ensure a smooth transition past the limit ordinal. We will consider the other possible stopping point here, namely the situation in which at a certain stage the set does not have a suitable retraction any more. (In finite ordered sets this is the only way the dismantling process stops.)
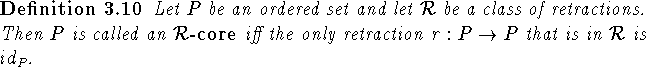
Easy examples show that a set can have many
cores (every singleton subset of a finite fence is a
-core of that fence), but one can
show the -core of a finite set is unique
up to isomorphism
(cf. [31], [39]).
Proof:
Let 
be such that 
.
Then since the set of points that are not fixed by f
has 
elements, there are distinct
such that 
. Choose
i<j both minimal such that .
Then 
and 
.
Moreover for all 
we have
Thus
Since 
for all fixed points of f, we are done
\
Proof:
For 
let 
be the smallest
ordinal such that 
for all 
. (Such 
exists since the family 
is infinitely composable.)
Now since 
, we have
\
Proof:
Part 1a is proved in [119], the finite
case being proved in [31] and in [39].
The proof is similar as the proof for part 2 that we are about
to present. Parts 1b and 1c
are easy as there is a largest up-retraction, resp. a
smallest down-retraction on every chain-complete ordered set.
For part 2
let 
be an 
-core
such that there is an infinite
-dismantling S of P onto C.
Let 
be an infinite -dismantling, which is
the infinite composition
of the -retractions 
.
We will prove inductively that
for all 
we have
.
For 
this is trivial
and for
a limit ordinal this follows from
Lemma 3.13.
If is a successor ordinal, note that
.
Since 
is an -retraction
and since 
is injective, we have that
.
Thus if
, then 
is a retraction by Lemma 3.12 and
.
Since C is an -core, this means that 
, i.e.,
that 
.
Thus 
.
Now suppose 
are -cores of
P with 
being an infinite
-dismantling to 
(i=1,2).
Then by the above 
and
, and hence 
and
are isomorphic.
For part 3
let
P be finite and let
be an 
-core
such that there is an
-dismantling S of P onto C.
Let be an -dismantling which is
the composition
of the -retractions ,
where 
is finite.
We will prove inductively that
for all
there is an order-preserving
mapping 
such that
.
For this is trivial
(choose 
)
and since is finite we do not need to consider limit ordinals.
If is a successor ordinal, note that
.
Since is an -retraction
and since is injective, we have that
.
Thus if
, then 
is a retraction by Lemma 3.12 and
.
Since C is an -core, this means that 
.
Thus 
is the map with
.
Since the dismantling of P stops after finitely many steps, there is
an order-preserving map R such that 
.
Now suppose are -cores of
P with being a finite dismantling to (i=1,2).
Then by the above there are order-preserving maps
such that 
and
.
Hence and
have the same number of elements.
But then 
is an isomorphism from
onto 
. \
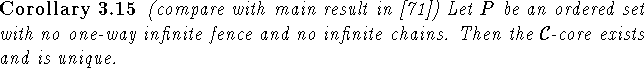
Proof:
Existence follows from the main theorem in [70], as
for ordered sets with no one-way infinite fence and no infinite
chains
infinite -dismantlability is equivalent to the notion of
dismantlability used in [70]. \
