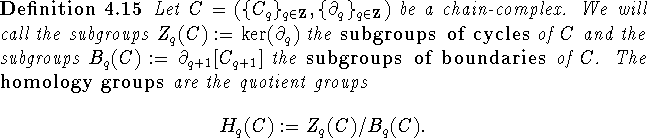
Here (specifically in Lemma 4.18) is ``where the miracle of algebraic topology occurs". Through Lemma 4.18 many Lefschetz numbers become computable and thus a host of combinatorially surprising fixed point theorems (many of which still have no combinatorial proof) enters the theory.
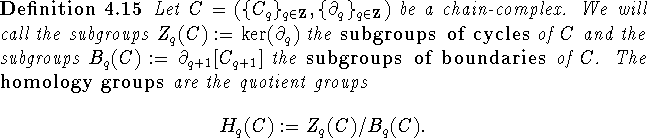
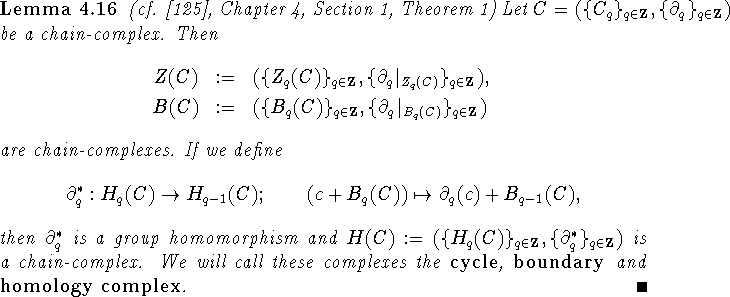
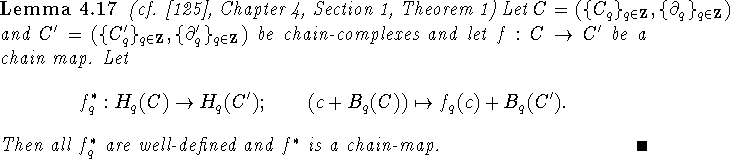
Proof:
First note that 
and
, since for
we have
while for 
there is an 
with
and thus
Now since 
and
(with 
being the
isomorphism) we have
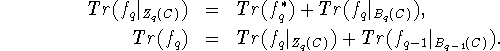
Adding the two equations, multiplying with
and summing over q gives the
equality of the Lefschetz numbers and the equality
of the Euler characteristics follows from
. \
Proof:
The generators for 
are the differences
v-w, where v,w are vertices of K with 
.
Thus if u,z are vertices in the same component of K, then
.
On the other hand if , then u-z must the the sum
of finitely many generators of and thus u and
z must be in
the same component of K.
Since 
, the vertex set of K, this implies
that any two vertices x,y in the same component of K
satisfy 
, while if
x' and y' are not in the same component of
K we have 
.
Hence 
has exactly k generators with no further
conditions to be satisfied, i.e., it is isomorphic to
. \
In particular this means that if K is connected, then
is isomorphic to 
.
If this is the only interesting homology group of K, we
will say that K is acyclic.
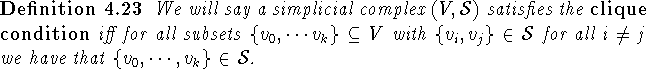
Clearly a simplicial complex is the clique complex of a graph iff it satisfies the clique condition (cf. [46], Proposition 4.4, or originally [125], Gikas also investigates the Euler characteristic of the chain complex of an ordered set in [46], Chapter 4).
Proof:
First note that if 
is a simplex
of K that does not contain x, then
.
On the other hand no nonzero sum of orientations of
simplexes that all contain x can ever be in 
.
Thus the cosets of the orientations of the simplexes that contain x
are a set of generators for 
with
no equations beyond 
for 
being an odd permutation
to be satisfied.
Let 
. If
is a simplex that contains
x, we can find a representative 
of
such that
.
Since any two such representatives only differ by an even permutation
of the indices up to q-1
we have that 
is a well-defined map
from the
set of orientations of simplexes that contain x to 
.
Since the orientations of simplexes
that contain x are a system of representatives for
the generators of and their inverses and since
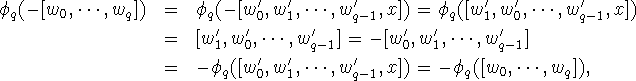
extends in a natural fashion to a homomorphism
from to , which we will
also call .
For q=1, we let 
,
and extend this in the natural fashion
to a homomorphism.
Surjectivity of follows from the clique condition and
if
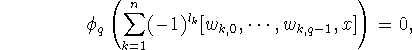
then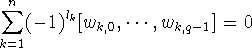 
, which implies that
Thus is an isomorphism
(for q=1 this is trivial).
To see the equation
for
consider:
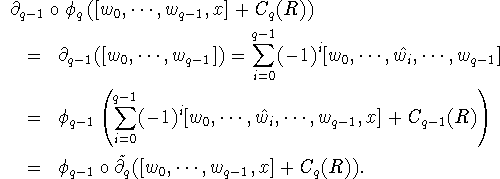
For the statement for the homology groups is now trivial.
For q=0 note that 
is the whole
group 
(which is generated by
) in case there is a 
such that
and that 
if not.
For q=1
note that
the generators of 
are the set
while the generators of 
are the set
Thus any difference
with a,c in the same component
of 
is in and no difference
with a,d in different components of
is in .
If is connected, then
clearly 
and
.
If is not connected,
let 
be the components of and let
be a vertex of 
.
Then the generators
( 
)
are mutually
distinct and there are no equations between them to be
satisfied. Moreover all other elements of 
are
sums of these generators and their inverses.
This proves the claim.
\
Theorem 4.25, which is an easy consequence of Lemmas 4.22 and 4.24, provides an algorithm to compute the homology of collapsible ordered sets. These are defined as follows.
Obviously (connected) collapsibility is a generalization of dismantlability. However while dismantlability of an ordered set can be determined in polynomial time, it is not clear if the same can be said for (connected) collapsibility (cf. open question 3). Connected collapsibility also gives some insight in the structure of the sets of fixed points of order-preserving maps (cf. Theorem 5.6). The definition of connectedly collapsible graphs is analogous and we can record:
Proof:
Let G=(V,E) be a connectedly collapsible
graph.
We prove the statement by induction on n=|V|.
For n=1 there is nothing to prove.
Now suppose 
and the result holds for all
graphs with 
.
Let G=(V,E) be a graph with |V|=n. Then
by the definition of connected collapsibility
there is an 
such that 
is a retract of
V, 
is connectedly collapsible and
is connectedly collapsible.
Then 
is not an empty graph (since the empty graph is not
connectedly collapsible). Thus
since both and have
at most n-1 vertices both are acyclic.
Thus by Theorem 4.25 G is acyclic.
\
Proof: Dismantlability implies connected collapsibility. \
Proof:
``2 
3" follows from
Theorem 4.27.
``3 1"
follows from Lemma 4.21.
Finally for ``1 2"
suppose P is collapsible and not connectedly collapsible.
We will prove by induction on n:=|P|
that P does not have the fixed point property.
For n=1 there is nothing to prove.
Suppose now n>1 and the result holds for all ordered sets
Q with
|Q|<n. Then there is a retractable point 
such that
is collapsible and not connectedly collapsible
or
is
collapsible and not
not connectedly collapsible. By induction hypothesis
this would mean that
does not have the fixed point property
or
does not have the fixed point property or it is empty
(in which case it also does not have the fixed point property).
This implies by Theorem 3.4 that P does not have the
fixed point property. \
Again clearly a similar result can be proved relating collapsibility of graphs to acyclicity and the fixed clique property.
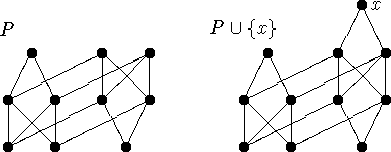
Figure 3: Figures to illustrate example 4.30.
It is finally worth recording that (obviously) since the homology of an ordered set and the associated complexes are defined through the comparability graph they all are comparability invariants and thus only useful in the study of other comparability invariants.
