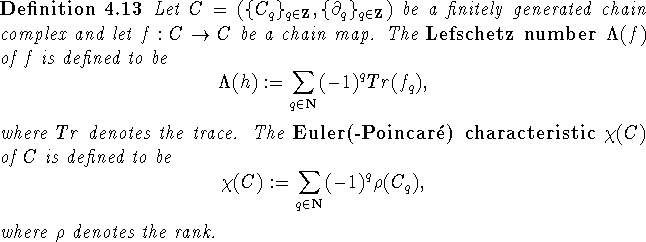
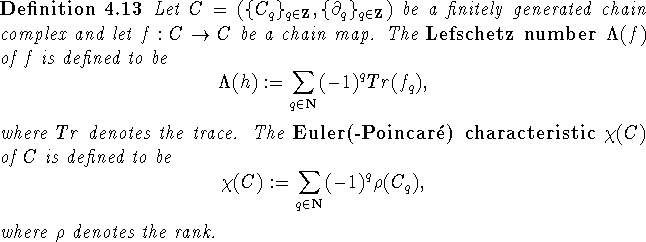
For fixed point theory the Lefschetz number of a map is interesting,
as it can be used as a sufficient criterion for the existence of
fixed points/cliques/simplexes:
Let 
be a simplicial map on the finite simplicial complex
. If 
, then there is a
such that 
.
Thus there is a q-dimensional simplex
such that
for some 
and h a
combination of the generators other than S.
However since
this means
.
Hence we have that
f[S]=S, i.e., f has a fixed simplex.
Now if K is a clique complex and f is induced by a
graph endomorphism, this means that there is a clique
C such that f[C]=C. If K is a P-chain complex
and f is an order-preserving map on P, then
f maps a chain to itself, which naturally means that
f has a fixed point.
The first arguments
by Baclawski and Björner
that link algebraic topology to
fixed points in
ordered sets
(cf. [7], Theorems 1.1, 1.2; [18], Théorème 1.1)
actually prove Lefschetz type theorems that state that
for an order-preserving map 
the Euler characteristic of the set
of fixed points of f is
equal to the Lefschetz number of f.
Thus we also gain an insight in the structure of
(also cf. section 5.3).
For breveties' sake we will not deepen this investigation here.
The above argument leads us naturally to two further
combinatorial properties worth considering:
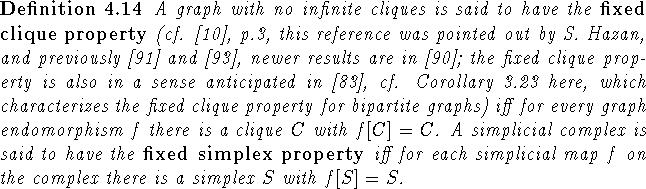
Clearly for ordered sets P with no infinite chains the fixed clique property for the comparability graph resp. the fixed simplex property for the P-chain complex both imply the fixed point property for P. Moreover all fixed point theorems for ordered sets that are derived using algebraic topology are fixed clique or even fixed simplex theorems. Combinatorial fixed clique theorems for finite graphs that are analogous to fixed point theorems for ordered sets have been derived in [120] (due to the fact that the definitions of graph endomorphisms and order-preserving maps are formally very similar this is not too hard). Further investigation of the fixed simplex property is complicated by the fact that there is no easy formal resemblance between the definition of an order-preserving map and a simplicial map (also cf. examples in [120]).