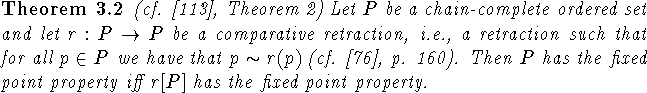
The initial work in this direction is found in the paper [95] by Rival, which has since been extended in various directions. We will present the best folklore version of Rival's original result in Theorem 3.2 and a modification in Theorem 3.4. Notice that chain-completeness is not needed in Theorem 3.4 and Scholium 3.5.
Proof:
The direction `` 
" follows from part 1 of
Theorem 3.1. To prove `` 
" let
be a comparative retraction and let 
be
order-preserving. Then
has a fixed point p and since
r is a comparative retraction
f(p) is related to p. Thus by the
Abian-Brown-Pelczar Theorem we have that f has a fixed point. \
