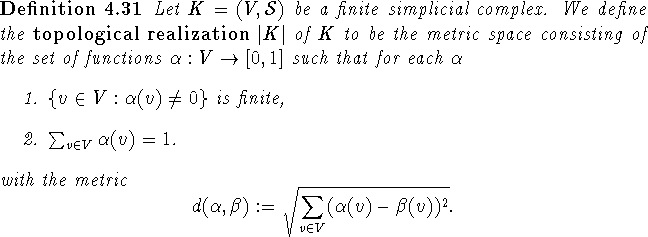
Theorem 4.25 can be viewed as a homological analogue of Theorem 3.4. Since the assumptions only require that the retraction is a weak retraction, it is now natural to look for conditions that ensure the existence of such a weak retraction. Most of the work in that direction has been done by Constantin and Fournier in [18]. The connection to topology is established through the topological realization of a simplicial complex:
Clearly the topological realization of a finite simplicial complex
can be embedded as a subspace in 
with the
usual topology.
Simplicial maps are extended to affine maps by affine interpolation.
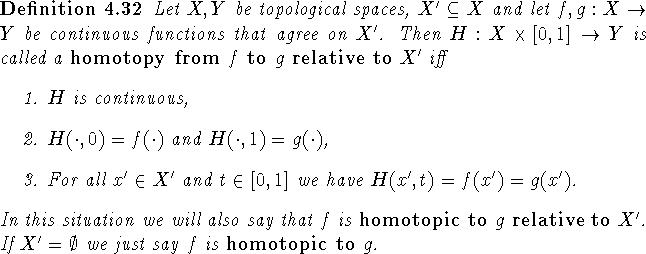
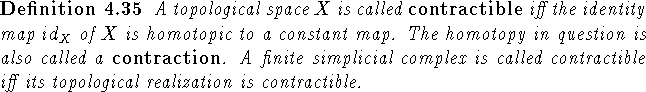
From Lemmas 4.22 and 4.24
we can easily infer that if 
is a
weak retract of |P| and 
is acyclic, then 
.
This can be seen as an underlying fact to the
work in [18] in which contractibility
(through Proposition 4.39)
plays a central role.
Proof:
The homotopy of 
to a retraction onto
relative to
is constructed as follows:
Let 
and
let 
be a contraction.
Then for each point 
there
are unique 
and 
such that
and
is a (strong) deformation retraction from |K| to
.
\
For any finite ordered set all the properties below make sense. They are listed such that the lower-numbered properties imply the higher-numbered ones. Similar lists can be made up for graphs and simplicial complexes.
has the fixed clique property,``P is connectedly collapsible" fits in between conditions 1 and 2 (cf. [122]).
