Close to the deadline for this article the author was mailed the
preprint [29], in which it is proved that problem
2.3 is indeed NP-complete.
One of the main obstacles to such a proof is the large number of
possibilities for order-preserving maps on an ordered set, which makes
a reduction to 3SAT difficult.
For example the sets used in the second proof of Theorem 2.14
are all dismantlable (cf. Example 3.9, part 1)
to a 2-8m complete bipartite ordered set
and thus do not have the fixed point property. In fact they have
many fixed point free order-preserving maps, while the possible
fixed point free automorphisms are restricted by many
constraints (which is of course what makes the argument work).
In [29] Duffus and Goddard
present a beautiful class of ordered sets that
is such that if a member has a fixed point free order-preserving map, then
it must have a very ``well-behaved" order-preserving map.
This nice structure then allows to embed another NP-complete problem
into ordered sets.
The ordered sets used in [29] are quite special, so
interesting questions regarding the complexity of the fixed point
property remain, as for example the questions in [29] and
questions 1 and
6 in section 5.7 indicate.
Regarding complexity of the fixed point property in general, one
might now be interested how difficult problem 2.3 is
``on average" (since NP-completeness is a worst
case concept). For an introduction to
average case complexity
cf. J. Wang's survey [130].
Also the sets in [29] can be used to
construct ordered sets with the fixed point
property for which Xia's reduction algorithm terminates with a
graph that still has edges:
In fact, the set
constructed from the non-satisfiable, 3-variable, 8-clause
instance of 3SAT has by [29] the fixed point property and
it was proved (in collaboration with M. Roddy)
that Xia's algorithm terminates with a graph that has edges left.
The ordered set in question has 434 points and its fixed-point-free
endomorphism graph has in excess of 80,000 vertices.
Presently no smaller sets with this property are known.
Again, for the proof that problem 2.3 is NP-complete
the reader is referred to [29], which is
self-contained and nothing short of a complete
reproduction could do it complete justice here.
Xia's ideas are a more versatile tool than indicated here:
If P,Q are finite sets (with possible additional structures),
then for any set of functions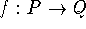 
that for all
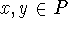satisfy
conditions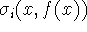 
and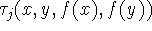 
( 
, 
,
, 
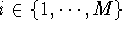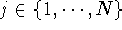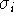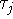logical propositions) we can construct the
Xia graph as follows: The vertices are all
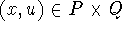such that all conditions
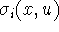are satisfied and the edges are all
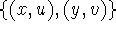such that all conditions
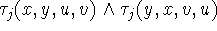are satisfied.
Then as in Theorem 2.7
we have a natural correspondence between these maps and
the maximum sized cliques in the Xia graph.
Xia's algorithm can be used and if it terminates with a graph with
no edges, there is no map satisfying all conditions.
If Xia leaves some edges, a subsequent depth-first search can settle
the question of existence, resp. determine the number of
maps.
Thus Xia's algorithm can be used as a (for existence problems highly
efficient) preprocessor when confronting problems such as:
Enumeration and existence of relation preserving self maps
with special properties, the isomorphism problem for graphs,
determination of rigidity of graphs or ordered sets,
existence of fixed point free automorphisms, etc.
All that is needed is a formulation of all the properties of the
maps as indicated above.
The magnitude of the improvement Xia provides in
various settings is currently under investigation
([26]). It appears that using Xia's algorithm
(plus depth-first search if necessary)
the
fixed point property for ordered sets with up to 100
points can be decided on a desktop PC with enough RAM.