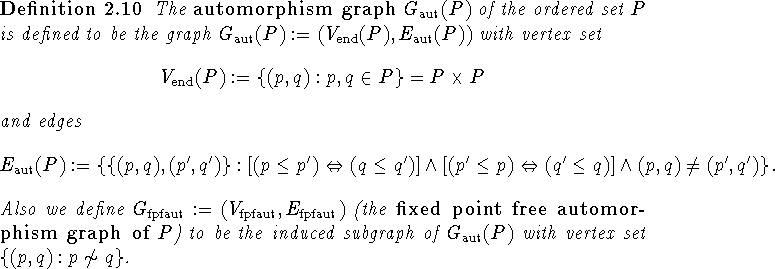Recall that a graph
is a pair G=(V,E) of a set V of vertices
and a set E of doubleton subsets of V, called
edges.
The induced subgraph of a graph G=(V,E) with vertex set
is the graph
.
Unless otherwise stated all subgraphs will be induced subgraphs.
The choice of language can be justified by the following
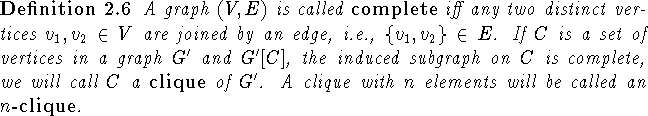
Proof:
`` 
": If 
is an order-preserving self map
then 
is in particular well-defined and thus
for all 
. Now let
.
Then since is order-preserving the logical
statement
is true and 
is an edge in 
.
`` 
":
Let 
be such that
the induced subgraph of with
vertex set is a complete graph with
for all .
The latter immediately shows that is well-defined, i.e.,
a function.
Now let 
with 
, 
.
If 
, then, since
is a true logical statement, we have 
.
Thus is order-preserving.
\
Based on criterion 2.7 various kinds of order-preserving self maps can be identified in the endomorphism graph.
Theorem 2.7 is applicable to infinite ordered sets.
For the computationally more interesting finite case the condition
for all p can be replaced with
the demand that has |P| vertices.
With regards to fixed point free order-preserving maps
on finite ordered sets we obtain:
Proof:
This follows directly from the analogue of
Theorem 2.7 for fixed point free order-preserving self maps.
Just note that
by Remark 2.5 any complete subgraph of
the endomorphism graph has at most one vertex in each 
.
\
In order to decide if a finite ordered set P has a fixed point
free order-preserving self map one would thus need to decide if
the fixed point free endomorphism graph has
a |P|-clique.
As mentioned in [65]
there currently
are algorithms that determine the maximal size of a
clique in a graph in acceptable time for graphs with up to
400 to 1000 vertices. As the fixed point free endomorphism
graph of P has at most |P|(|P|-1) vertices and normally actually
fewer than that, this means the fixed point property can be
determined through the fixed point free endomorphism graph for
ordered sets with up to 20 (guaranteed) to (possibly)
50 or more points.
To
decide if a finite ordered set P has a fixed point
free automorphism one would need to decide if
the fixed point free endomorphism graph has
a complete induced subgraph as described in
part 3
of Proposition 2.8 and Corollary 2.9.
To get a completely analogous formulation consider:
