In May-June 1996 results that give algebraic, resp. combinatorial proofs
for the result that every finite truncated noncomplemented
lattice has the fixed point property
were announced by K. Baclawski in [6] and by
T. McKee and E. Prisner in [80].
We will present McKee and Prisner's approach here as their
methods are natural applications of what is discussed in this chapter.
The following is thus nothing but a translation of
the results in [80]
from their original version for modulo 2 homology to integer homology.
It becomes necessary, since the beautiful geometric approach
to homology
in [80] seems to depend on the fact that -1=1 in ![]() ,
while the arguments generalize beyond this visualization. One just
needs to carefully keep track of the signs at times.
,
while the arguments generalize beyond this visualization. One just
needs to carefully keep track of the signs at times.
Proof:
In case q=1, there is nothing to prove (the boundary of a
sum of zero-dimensional simplexes is 0).
Let ![]() be a (q-2)-dimensional oriented simplex that
occurs in one of the (q-1)-dimensional simplexes
be a (q-2)-dimensional oriented simplex that
occurs in one of the (q-1)-dimensional simplexes
![]() , with
, with ![]() .
Then
.
Then
![]() occurs once
(positive or negative)
in
occurs once
(positive or negative)
in
![]() , but by assumption
it does not occur in
, but by assumption
it does not occur in
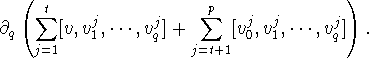 Therefore
Therefore
![]() occurs in an even
number, say 2k, of the
occurs in an even
number, say 2k, of the
![]() (
( ![]() )
and it occurs such that
in k
of the
)
and it occurs such that
in k
of the
![]() the summand
the summand
![]() is positive
and in the other k boundaries
it is negative.
If
is positive
and in the other k boundaries
it is negative.
If
![]() is a positive summand of
is a positive summand of
![]() , then
, then
![]() is a negative summand of
is a negative summand of
![]() and
vice versa.
Thus no multiple of
and
vice versa.
Thus no multiple of
![]() occurs in
occurs in
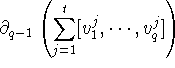 by the observed cancellation.
The conclusion follows.
\
by the observed cancellation.
The conclusion follows.
\
Proof:
Assume ![]() ,
,
![]() .
If q=1 assume
.
If q=1 assume
![]() ,
if
,
if ![]() assume
assume
![]() .
.
First, we show that every homology class of q-dimensional cycles
has a representative that does not contain v.
Assume ![]() .
Let
.
Let
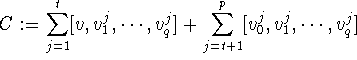 be a representative of the homology class
be a representative of the homology class
![]() ,
with
,
with ![]() .
If t=0, we are done, so we can assume
.
If t=0, we are done, so we can assume ![]() .
By Lemma 4.53,
.
By Lemma 4.53,
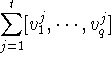 is a (q-1)-cycle of G and hence also of
is a (q-1)-cycle of G and hence also of
![]() .
Since
.
Since
![]() there are q-simplexes
there are q-simplexes
![]() ,
, ![]() ,
,
![]() of
of
![]() such that
such that
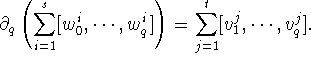 But then
But then
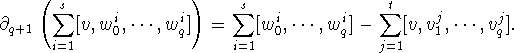
Thus
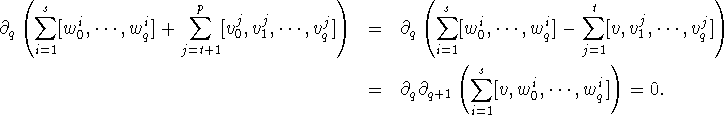
Thus
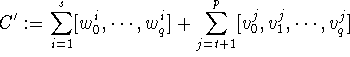 forms a q-dimensional cycle with
vertices in
forms a q-dimensional cycle with
vertices in ![]() .
Finally C and C' are homologous, since
.
Finally C and C' are homologous, since
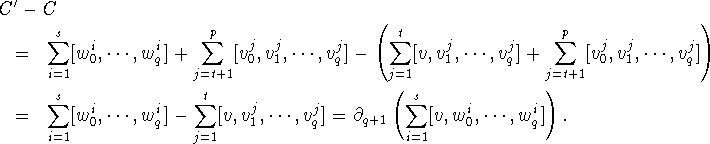
In case q=1,
let
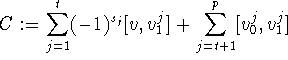 be a representative of the homology class
be a representative of the homology class
![]() ,
with
,
with ![]() .
t must be even, say t=2k and
k of the
.
t must be even, say t=2k and
k of the ![]() must be 0, the rest 1
(otherwise the boundary of C contains a multiple of [v]).
Since
must be 0, the rest 1
(otherwise the boundary of C contains a multiple of [v]).
Since
![]() , we have by Lemma 4.19
that
, we have by Lemma 4.19
that
![]() is connected.
However then
is connected.
However then
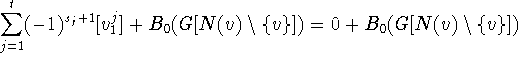 , since
in a connected graph
any sum of differences of zero-dimensional
simplexes is the boundary of a sum of 1-dimensional
simplexes.
Now the argument continues as in the case
, since
in a connected graph
any sum of differences of zero-dimensional
simplexes is the boundary of a sum of 1-dimensional
simplexes.
Now the argument continues as in the case
![]() .
.
If we can show now that for any q-cycles
C,C' that do not contain v we have
![]() iff
iff
![]() then the map that maps
every homology class
then the map that maps
every homology class ![]() in
in
![]() to the corresponding homology
class in
to the corresponding homology
class in ![]() defined by the
representatives of
defined by the
representatives of ![]() that do not contain v
is an isomorphism and we are done.
To do so first note that the
direction ``
that do not contain v
is an isomorphism and we are done.
To do so first note that the
direction `` ![]() " is trivial.
For the other direction let
" is trivial.
For the other direction let
![]() with
with
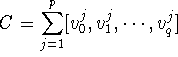 with
with ![]() .
Then
.
Then
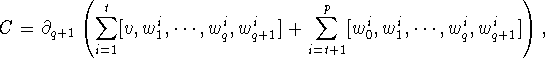
with ![]() .
By Lemma 4.53
.
By Lemma 4.53
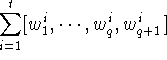 is a q-cycle and since
is a q-cycle and since
![]() there must be (q+1)-dimensional simplexes in
there must be (q+1)-dimensional simplexes in
![]() such that
such that
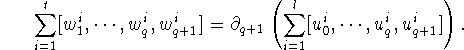
But then
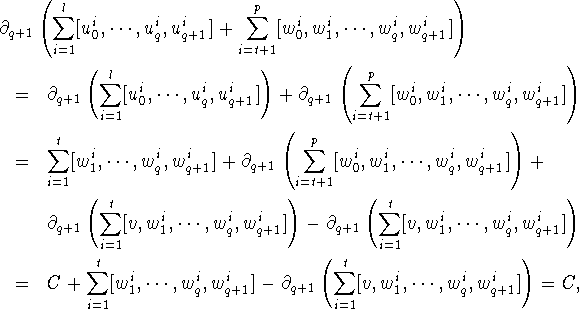
with the cancellation in the last step happening since
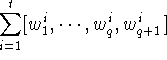 is a cycle in
is a cycle in ![]() .
This finishes the proof.
\
.
This finishes the proof.
\
This together with the removal of escamotable points as
discussed in section 4.5
gives a proof of Baclawski and Björner's
result that is entirely algebraic.
(Contractibility of the neighborhood was needed to
guarantee removability of the point without affecting the homology.
The contractibility of escamotable graphs was a nice consequence, which
is however stronger than what was needed.
A notion ``vertex is weakly escamotable iff its pointed neighborhood
is acyclic" is strong enough for our purposes.)
Baclawski's argument (cf. [6]) proves a result
similar to Corollary 4.55
about structures called ``pseudo cones" using neither algebra,
nor topology. His fixed point algorithm for pseudo cones
does not use any previously known method
and as with [29] we refer the reader to the original.