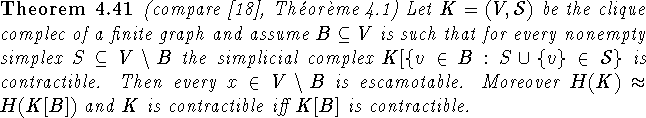
Proof:
This is an induction on ![]() . For
n=0 there is nothing to prove.
So now let n>0 and suppose the result holds for
all k<n.
Let
. For
n=0 there is nothing to prove.
So now let n>0 and suppose the result holds for
all k<n.
Let ![]() and let
and let
![]() ,
,
![]() and let
and let
![]() .
Then K' and B' satisfy the hypothesis of the theorem:
In fact if
.
Then K' and B' satisfy the hypothesis of the theorem:
In fact if ![]() is a simplex in K', then
by the clique condition
is a simplex in K', then
by the clique condition
![]() is a simplex in K and
again via the clique condition
is a simplex in K and
again via the clique condition
![]()
where the latter simplicial complex is contractible.
Moreover ![]() is contractible by assumption.
Now since
is contractible by assumption.
Now since ![]() by induction hypothesis
K' is contractible and thus x is escamotable.
by induction hypothesis
K' is contractible and thus x is escamotable.
To prove the ``moreover" part we need to prove that
K is ``dismantlable via escamotable points" to
K[B]. To see this it is good enough to show that
![]() and B satisfy the assumption of the theorem.
Let
and B satisfy the assumption of the theorem.
Let ![]() be a simplex.
Then
be a simplex.
Then
![]() is contractible by assumption and we are done.
\
is contractible by assumption and we are done.
\
Clearly a set B as above must intersect every maximal simplex, which is exactly the notion of a cutset.

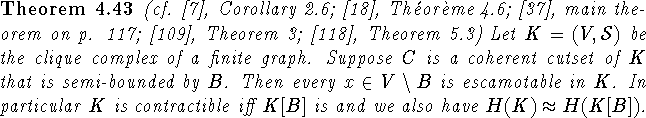
Proof:
We will prove that the simplicial complex satisfies the
assumption
of Theorem 4.41.
Let ![]() be a simplex.
Then the set
be a simplex.
Then the set ![]() has a center and is thus contractible. \
has a center and is thus contractible. \