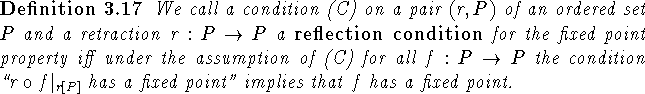
Proof:
First note that since
is a retraction the condition
``P has the fixed point property" implies that
has the fixed point property for all 
.
For the other direction let 
be order-preserving.
Then 
has a fixed point p.
We will prove inductively for all
that the condition `` 
has a fixed point p" implies
that
f has a fixed point.
For 
this is trivial.
Now let 
and assume the assertion holds for all
. First suppose is a
successor ordinal. If
has a
fixed point then
(since 
satisfies a reflection condition)
has a
fixed point.
By induction hypothesis the latter implies that f has a fixed point.
Finally if is a limit ordinal
suppose that
has a fixed point p.
Then there is a 
such that
.
Thus 
has p as a fixed point and
by induction hypothesis f has a fixed point. \
Theorem 3.19 obviously leads to an algorithm for a sufficient
condition for the fixed point property:
Dismantle P via 
-retractions as far as possible and
verify a reflection condition at every step.
Any set for which this is possible with a core that has the fixed point
property has the fixed point property itself.
The difficulty in finding reflection conditions however is considerable
as can be seen in [118].
Infinite-dismantlability also gives an algorithmic insight
into a classical result about the fixed point property
for ordered sets of height 1 (recall that the height of an
ordered set P is the number of elements in the largest chain
in P minus 1):
Proof:
Assume P does not contain an irreducible point.
Let 
be arbitrary and minimal.
Let 
be an upper cover of 
.
Assume that 
have already been chosen and
is a fence.
We will assume without loss of generality that 
is minimal.
Then has an upper cover 
. Choose
. Then since P does not contain any crowns
is a fence.
In this fashion we can construct an infinite fence in P,
contradiction. \
Proof:
``1 
2":
Necessity of connectedness is trivial.
If P contains a crown
P cannot have the fixed point property as is proved in
[95], p. 312 ff. (the argument given never uses that P is finite).
Thus P contains no crowns.
Were P to contain an infinite fence F and no crowns, then F is
an isometric spanning fence and hence by Theorem 2 in [34] it is
a retract (this is also easy to see directly).
This would again imply that P does not have the
fixed point property. Hence 2 must hold.
``2 3":
Let 
.
Suppose 
is an ordinal number and 
as in
Definition 3.7
have already been defined for 
.
If has a predecessor
such that 
is not a singleton, then there is a
point 
that is irreducible. Let 
be the retraction that
removes x and let 
.
If is a limit ordinal notice that since P does not contain
any infinite fences for each 
the sequence 
as in Definition
3.7
must be constant for 
for some 
.
We define 
.
If is a singleton we stop.
The sequence thus generated is an infinite dismantling of P.
``3 1"
follows from Theorem 3.19. \
Theorem 3 in [82], which is used to prove Theorem 4 in [82] (which is Theorem 3.21 here) can now be obtained via one of the standard translation processes between ordered sets and graphs (similar to what is done in [82]).
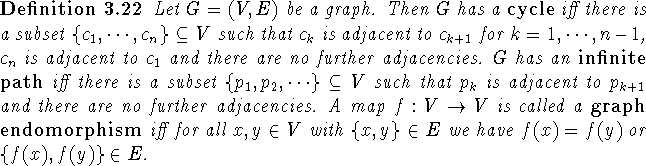
Proof:
(Compare with the idea of the proof of
Theorem 2.14.)
Let G=(V,E) be a graph.
We define an ordered set of height 1 with underlying set
and with the order being
containment of sets.
Let 
be a graph endomorphism of G. Then
is an order-preserving map of P.
Moreover if
F has a fixed point
that is minimal in P, then
f fixes v. If F
fixes no singleton, but
has a fixed point
that is maximal in
P, then f fixes .
Thus if
P has the fixed point property, then every endomorphism of G
fixes an edge or a vertex.
Let 
be an order-preserving map of P that maps the
minimal elements to minimal elements.
If for 
we let H(x) be the unique element of
the singleton set h(x), then
H is a graph endomorphism of G.
Moreover if H has a fixed vertex, then
clearly h has a fixed point, and if
H has a fixed edge , then
and hence 
.
Thus if every endomorphism of
G has a fixed vertex or a fixed edge, then
every order-preserving map of P that maps minimal elements
to minimal elements has a fixed point and
consequently P has the fixed point property.
Hence P has the fixed point property iff
every endomorphism of G has a fixed edge or a fixed vertex.
However by Theorem 3.21 P has the fixed point
property iff P is connected and has no crowns and no infinite
fences.
This is the case exactly when G is connected and has no
cycles with 
elements and no infinite paths.
Finally note that
G is
-infinite-dismantlable
to a singleton iff P is.
\
