
The Li-Milner structure theorem is a quite surprising result, as it states that in essence every chain-complete ordered set with no infinite antichain is an ``inflated finite ordered set". The first proof of this result in [74] is quite complex. For a shorter proof see Farley's paper [40]. We do not present a proof here, but instead show in Example 5.3 that unfortunately the assumption of chain-completeness in Theorem 5.1 cannot be relaxed. Still there are many interesting questions related to the Li-Milner theorem (cf. [40], [70]-[77], and open question 12 here).
As a corollary we can derive the algorithmic part of Fofanova and Rutkowski's result on ordered sets of width 2 in full generality.
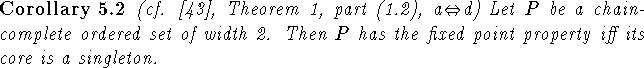
Proof: An ordered set P as desired has a finite core by Theorem 5.1. By Corollary 3.29 this core must be a singleton if P has the fixed point property. \
Figure 4: The ``Tower of Doom"