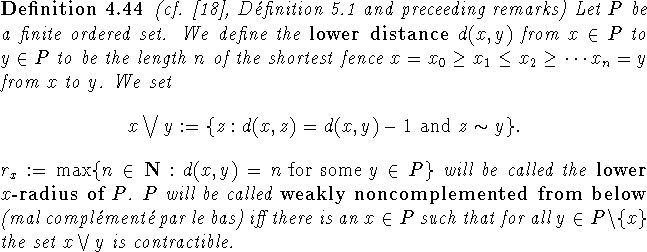
One of the most intriguing results in the fixed point theory of ordered sets is Baclawski and Björner's result that every finite truncated noncomplemented lattice has the fixed point property. The original proof (cf. [7], Corollary 3.2) is quite complex (it ultimately goes back to the intricate topological arguments in [11], Theorem 3.2, resp. to the arguments in [5], Corollary 6.3) and seems to be not algorithmic. The reduction arguments of Constantin and Fournier can be used to give another proof of this result. Interestingly even though Baclawski and Björner's result is topological and should thus have analogues for the fixed simplex and the fixed clique property, we need to assume that we are working with ordered sets for this proof.
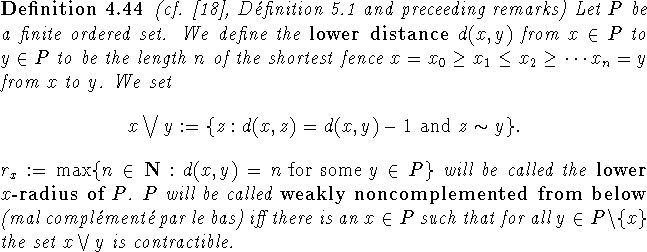
Baclawski and Björner's classical result now easily follows from:
Proof:
The proof is an induction on 
, the lower x-radius of P, with
x as in the definition of weak noncomplementedness from below.
For 
there is nothing to prove as P has a largest element.
Now assume that 
and the theorem holds for all
weakly noncomplemented from below sets P with 
.
Then 
is weakly noncomplemented from
below and
thus contractible.
It is thus sufficient to verify that the conditions of Theorem
4.41 are satisfied. (This is again a nice exercise in the
translations between ordered sets, graphs and simplicial complexes.)
We can assume without loss of generality that n is even.
Let C be a chain in 
and let y be the largest element
of C.
Then there is a fence
from x to y.
We will now show that
,
which is contractible, thus concluding the proof:
Let 
be such that 
is a chain.
Then 
.
Moreover since v is comparable to y we infer 
.
Thus d(x,v)=n and thus 
.
Conversely if , then d(x,v)=n, so .
Moreover we must have v> y (otherwise 
), which means
that is a chain. \
