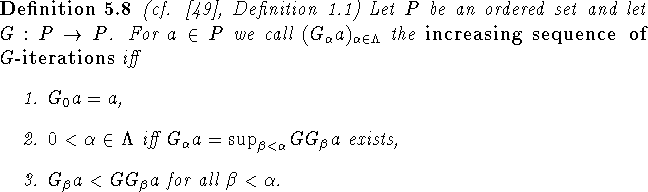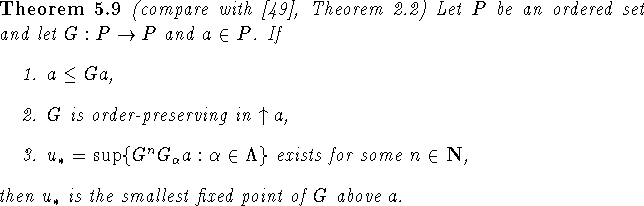



Next: Distance Problems
Up: Applications/New Directions
Previous: Clique Graphsk-null Ordered
The cornerstone of applications of order-theoretical
fixed point methods to analysis so far
appears to be the Abian-Brown-Pelczar theorem:
In a chain-complete ordered set P every order-preserving map for which
there is a 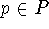 with
with 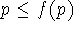 has a fixed point.
Abian and Brown prove it in [2] as a result on ordered sets.
Pelczar in the introduction of
[84] mentions the possible application to
integral inequalities, but gives no specific examples.
Recently these methods have been used sucessfully by Heikkilä,
Lakhshmikantham, Carl and Sun to prove existence results for
solutions for various differential and integral equations
(cf. [16], [17], [49]-[57]).
Similar iterations are used by Heikkilä and Salonen
to derive results in game theory (cf. [58]).
Due to the often very specific nature of results in nonlinear
analysis we will only present one example and the order-theoretical
iteration method that is used. The presentation is only intended
to give a general idea of the arguments
(the order-theoretical results can be derived fairly
quickly and for a complete introduction to nonlinear
analysis there certainly is not enough room in this paper).
For precise proofs the
reader is referred to [49]. For a larger set of results and
references cf. the text [56].
has a fixed point.
Abian and Brown prove it in [2] as a result on ordered sets.
Pelczar in the introduction of
[84] mentions the possible application to
integral inequalities, but gives no specific examples.
Recently these methods have been used sucessfully by Heikkilä,
Lakhshmikantham, Carl and Sun to prove existence results for
solutions for various differential and integral equations
(cf. [16], [17], [49]-[57]).
Similar iterations are used by Heikkilä and Salonen
to derive results in game theory (cf. [58]).
Due to the often very specific nature of results in nonlinear
analysis we will only present one example and the order-theoretical
iteration method that is used. The presentation is only intended
to give a general idea of the arguments
(the order-theoretical results can be derived fairly
quickly and for a complete introduction to nonlinear
analysis there certainly is not enough room in this paper).
For precise proofs the
reader is referred to [49]. For a larger set of results and
references cf. the text [56].
The underlying order-theoretical iteration used is similar in spirit to
Abian's f-chains (cf. [1]) respectively
Cousot and Cousot's iteration in [20] and [21].
Note however that it is neither assumed here that the function
is order-preserving, nor that the underlying set is
chain-complete.
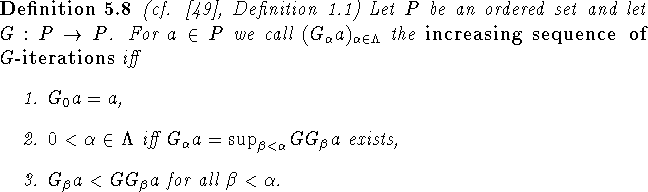
Clearly this sequence would be the
maximal sequence generated by
a
transfinite iteration
scheme (cf. [49], Lemma 1.1) such that
-
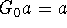 ,
, -
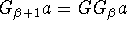 iff
iff 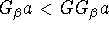 ,
, -
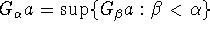 if
if
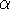 is a limit ordinal,
is a limit ordinal,
where the iteration stops when one of the steps
2 or 3 cannot be carried out. As noted in Theorem 1.1 in [49], the increasing sequence
of G-iterations always exists and is unique.
Moreover the proof of this result does not depend on the Axiom
of Choice (a similar point was made in [1] for the Abian-Brown-Pelczar
theorem). Unfortunately due to the extremely weak hypotheses the sequence
might have only one element, which need not be a fixed point.
However ([49], Lemma 2.1) if the increasing sequence of
G-iterations has a last element
As noted in Theorem 1.1 in [49], the increasing sequence
of G-iterations always exists and is unique.
Moreover the proof of this result does not depend on the Axiom
of Choice (a similar point was made in [1] for the Abian-Brown-Pelczar
theorem). Unfortunately due to the extremely weak hypotheses the sequence
might have only one element, which need not be a fixed point.
However ([49], Lemma 2.1) if the increasing sequence of
G-iterations has a last element 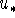 such that
such that
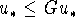 , then
, then 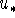 is a fixed point of G.
(Otherwise we could extend the sequence by adding
is a fixed point of G.
(Otherwise we could extend the sequence by adding 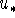 contradicting the maximality of the sequence.)
contradicting the maximality of the sequence.)
Unfortunately this result still is too general to be of much
apparent use, as the iteration could stop at any
successor or limit ordinal and the stopping need not guarantee a
fixed point. Introducing the hypothesis of being order-preserving
however one obtains the following variant of the
Abian-Brown-Pelczar theorem:
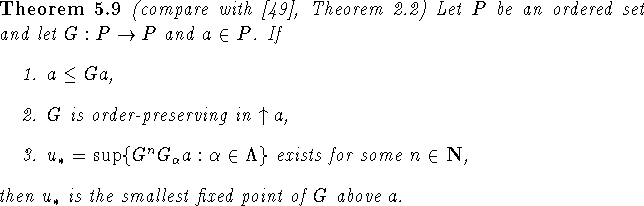
Condition 2 insures that nothing goes wrong at successor
ordinals and condition 3 insures the existence of all
needed suprema.
Condition 3 looks a little strange to the order-theorist,
especially considering that ([49], Lemma 2.2) it is equivalent to
the simpler condition 3 with n=0. However when applying
the result in analysis it is sometimes easier to prove condition 3
for an 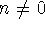 than it would be to prove it for n=0.
The included example of a Hammerstein integral equation is
an example.
This explains the format of condition 3.
than it would be to prove it for n=0.
The included example of a Hammerstein integral equation is
an example.
This explains the format of condition 3.
It would be interesting to see how far this idea can
be taken under mild hypotheses on the underlying ordered set.
It is easy to see that every space 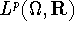 , where
, where
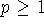 and
and
 is a measure space, is conditionally complete
(i.e., every set with an upper bound has a lowest upper bound) with
the pointwise almost everywhere order.
Thus conditional completeness might be a good hypothesis.
Then one could try to devise an iteration as described above
also for the case for which
is a measure space, is conditionally complete
(i.e., every set with an upper bound has a lowest upper bound) with
the pointwise almost everywhere order.
Thus conditional completeness might be a good hypothesis.
Then one could try to devise an iteration as described above
also for the case for which 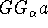 is not comparable
to
is not comparable
to 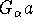 : As long as all is bounded above, take the supremum
as the next element of the sequence.
This is similar to the approach in [21], yet the author would
hope that milder conditions than assuming the underlying set is a complete
lattice would lead to success.
: As long as all is bounded above, take the supremum
as the next element of the sequence.
This is similar to the approach in [21], yet the author would
hope that milder conditions than assuming the underlying set is a complete
lattice would lead to success.
As an example let us consider the
following Hammerstein integral
equation
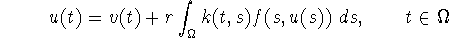
which is considered in [49], section 3.
 is a closed and bounded subset of
is a closed and bounded subset of 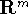 and all
functions except k assume values in an ordered Banach space
and all
functions except k assume values in an ordered Banach space
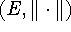 with
a closed and regular positive cone K.
(One could envision
with
a closed and regular positive cone K.
(One could envision 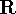 with its natural order here to
assimilate the general flavor of the following.)
Now assume:
with its natural order here to
assimilate the general flavor of the following.)
Now assume:
-
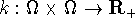 (i.e., k does not take negative values) is continuous,
(i.e., k does not take negative values) is continuous, -
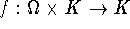 (i.e., f takes values
(i.e., f takes values 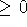 in E)
is such that
in E)
is such that
-
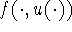 is strongly measurable for each
is strongly measurable for each
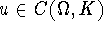 ,
, -
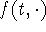 is increasing for almost every
is increasing for almost every 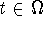 ,
, -
There are
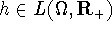 and a Bochner-integrable
and a Bochner-integrable
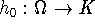 such that for all
such that for all 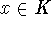 and almost every
and almost every
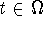 we have
we have
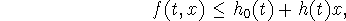
-
r>0 is such that
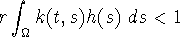 for each
for each 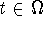 .
.
Then for each 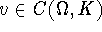 the above integral
equation has a solution.
the above integral
equation has a solution.
Clearly the operator to work with is
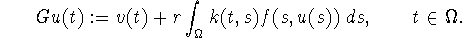
The fact that k maps into 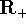 and f maps into K insures
that
and f maps into K insures
that 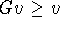 .
Condition 2b insures that G is order-preserving.
Condition 3
together with condition
2c insures (via an analytical argument) that there is
function
.
Condition 2b insures that G is order-preserving.
Condition 3
together with condition
2c insures (via an analytical argument) that there is
function 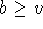 such that
such that
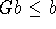 . Thus G maps
. Thus G maps 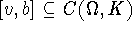 to itself.
Unfortunately this interval is not chain-complete, so we are not
trivially done. As done in section 3 of [49] a short analytical
argument shows that condition
3 of Theorem 5.9 is satisfied with n=1.
This proves that G has a fixed point and thus that the equation
in question has a solution.
to itself.
Unfortunately this interval is not chain-complete, so we are not
trivially done. As done in section 3 of [49] a short analytical
argument shows that condition
3 of Theorem 5.9 is satisfied with n=1.
This proves that G has a fixed point and thus that the equation
in question has a solution.
It can be proved that the set of all functions on
[0,1] that are constant on intervals bounded by dyadic
rationals and take dyadic rational numbers as values
forms a pseudo cone as defined in [6].
This construction is such that the restriction of the
pseudo cone structure to natural subsets, such as functions
constant on intervals bounded by dyadic
rationals of order n (denominator at most 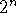 ),
taking dyadic rational numbers of order n as values,
also is a pseudo cone.
The domain [0,1] is chosen for convenience only.
Thus there is a possibility that Baclawski's algorithm
for pseudo cones can have further impact on
the use of order in analysis.
),
taking dyadic rational numbers of order n as values,
also is a pseudo cone.
The domain [0,1] is chosen for convenience only.
Thus there is a possibility that Baclawski's algorithm
for pseudo cones can have further impact on
the use of order in analysis.




Next: Distance Problems
Up: Applications/New Directions
Previous: Clique Graphsk-null Ordered
Bernd.S.W.Schroder