In [48] S. Hazan and V. Neumann-Lara investigate clique
graphs: If G=(V,E) is a graph, then its
clique graph k(G)
has the maximal cliques of G as vertices and two
maximal cliques are connected
by an edge iff they intersect.
An ordered set is called k-null
iff there is an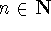 
such that the n-th
iterated clique graph of the comparability graph
is the one point graph.
They prove that k-null ordered sets have the fixed point property.
This result provides a new algorithm to approach the fixed point property,
namely by computation of clique graphs.
The theory in that direction seems to be unexplored and even though
the algorithm might be inefficient, the connection is
quite surprising and very interesting.