*Generalizations
• RedefinableElement (from Kernel ) on page 132
• Vertex (from BehaviorStateMachines ) on page 605
Description
State in Behavioral State machines
A state models a situation during which some (usually implicit) invariant condition holds. The invariant may represent a static
situation such as an object waiting for some external event to occur. However, it can also model dynamic conditions such as
the process of performing some behavior (i.e., the model element under consideration enters the state when the behavior commences
and leaves it as soon as the behavior is completed).
The following kinds of states are distinguished:
• Simple state,
• composite state, and
• submachine state.
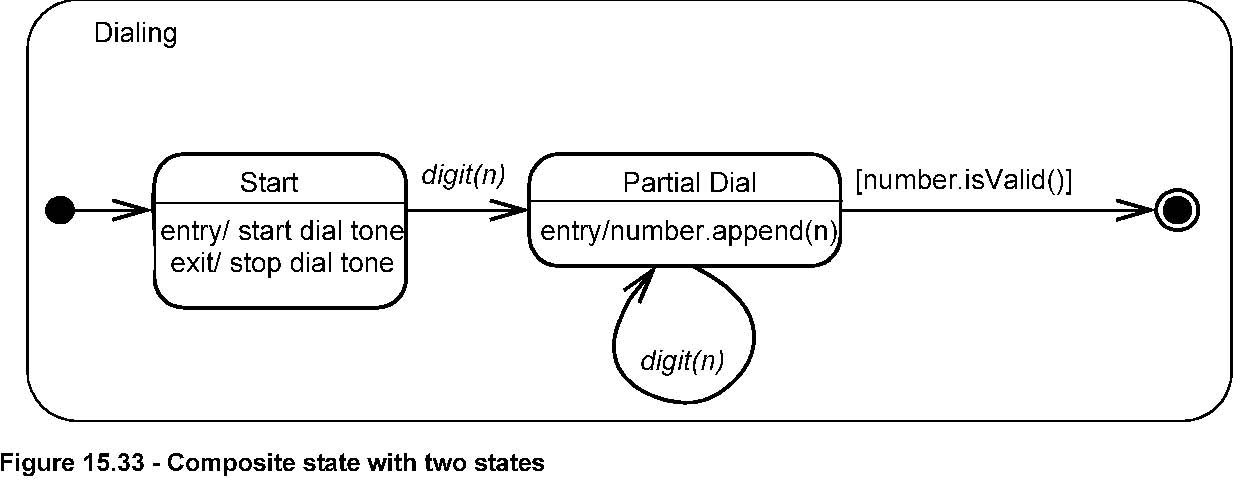
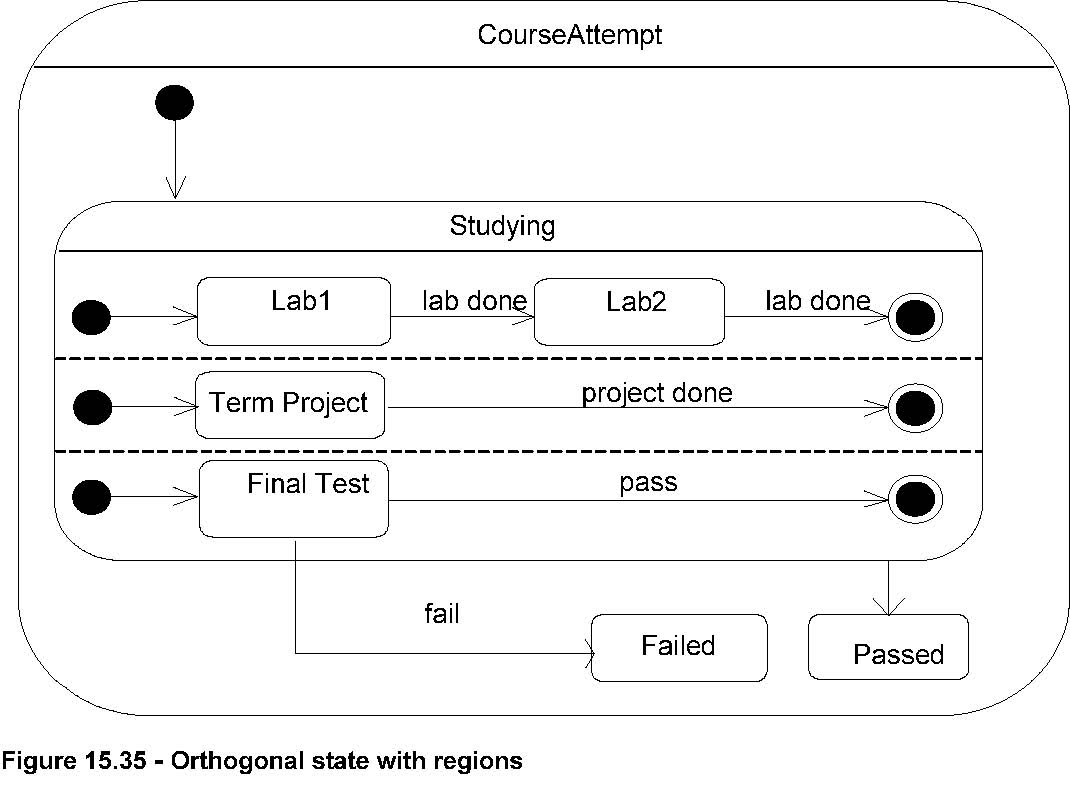
A composite state is either a simple composite state (with just one region) or an orthogonal state (with more than one region).
Simple state
A simple state is a state that does not have substates (i.e., it has no regions and it has no submachine state machine).
Composite state
Issue 8415 -add explanation and pointer to figure
A composite state either contains one region or is decomposed into two or more orthogonal regions. Each region has a set of
mutually exclusive disjoint subvertices and a set of transitions. A given state may only be decomposed in one of these
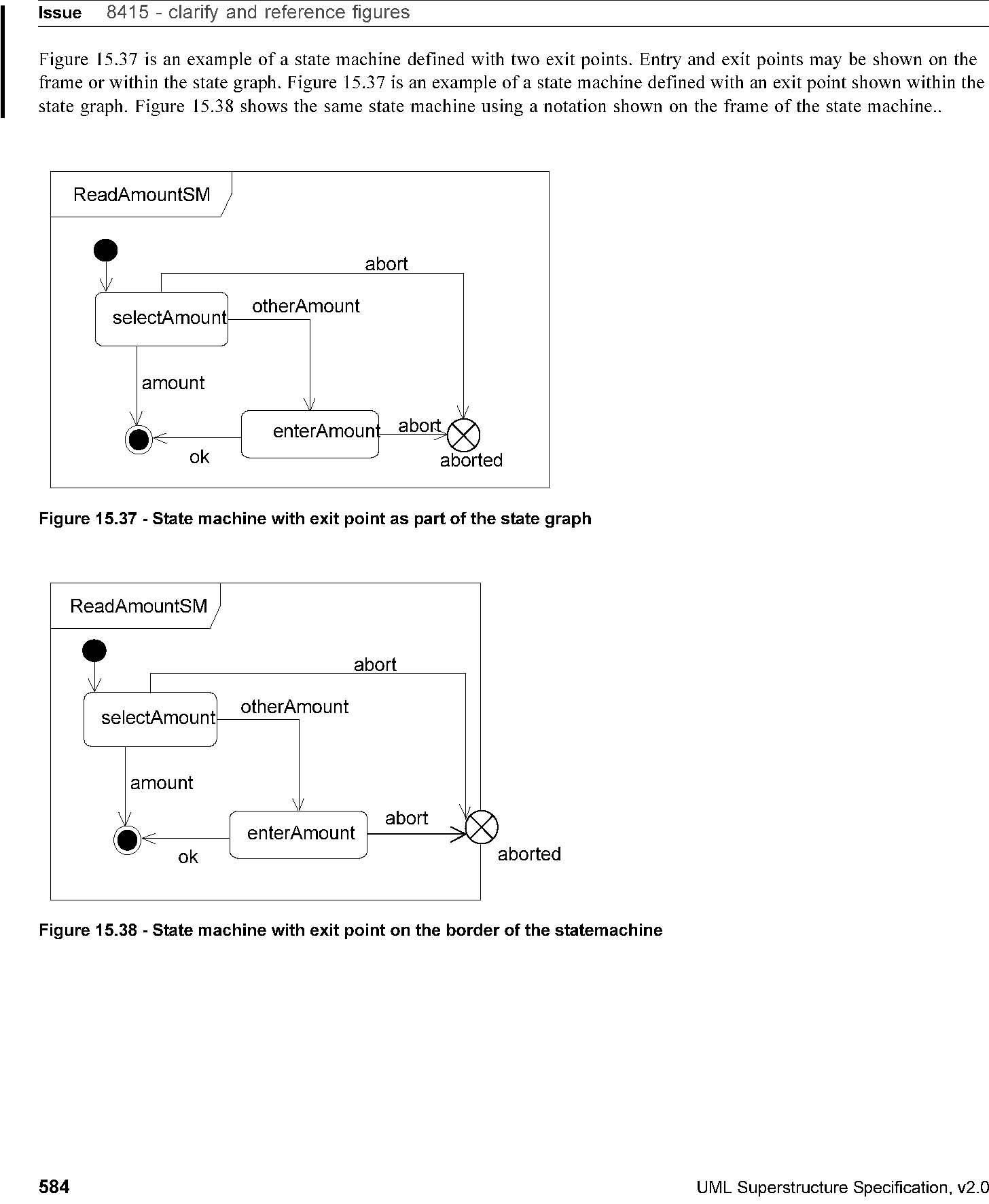
two ways. In Figure 15.35 on page 582, state CourseAttempt is an example of a composite state with a single region,
whereas state Studying is a composite state that contains three regions
Any state enclosed within a region of a composite state is called a substate of that composite state. It is called a direct
substate when it is not contained by any other state; otherwise, it is referred to as an indirect substate.
Each region of a composite state may have an initial pseudostate and a final state. A transition to the enclosing state represents
a transition to the initial pseudostate in each region. A newly-created object takes its topmost default transitions, originating
from the topmost initial pseudostates of each region.
A transition to a final state represents the completion of behavior in the enclosing region. Completion of behavior in all
orthogonal regions represents completion of behavior by the enclosing state and triggers a completion event on the enclosing
state. Completion of the topmost regions of an object corresponds to its termination.
An entry pseudostate is used to join an external transition terminating on that entry point to an internal transition emanating
from that entry point. An exit pseudostate is used to join an internal transition terminating on that exit point to an external
transition emanating from that exit point. The main purpose of such entry and exit points is to execute the state entry and
exit actions respectively in between the actions that are associated with the joined transitions.
Semantic variation point (default entry rule)
If a transition terminates on an enclosing state and the enclosed regions do not have an initial pseudostate, the interpretation
of this situation is a semantic variation point. In some interpretations, this is considered an ill-formed model. That is,
in those cases the initial pseudostate is mandatory.
An alternative interpretation allows this situation and it means that, when such a transition is taken, the state machine
stays in the composite state, without entering any of the regions or their substates.
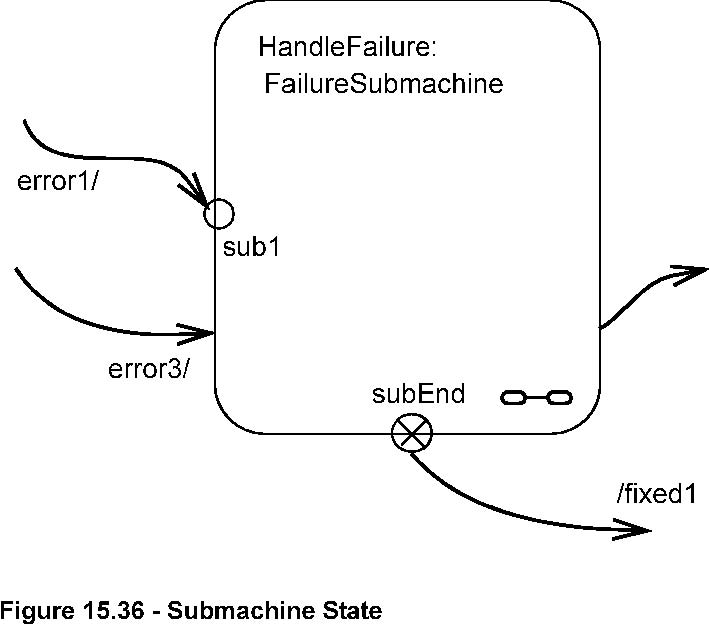
Submachine state
A submachine state specifies the insertion of the specification of a submachine state machine. The state machine that contains
the submachine state is called the containing state machine. The same state machine may be a submachine more than once in
the context of a single containing state machine.
A submachine state is semantically equivalent to a composite state. The regions of the submachine state machine are the regions
of the composite state. The entry, exit, and behavior actions and internal transitions are defined as part of the state. Submachine
state is a decomposition mechanism that allows factoring of common behaviors and their reuse.
Transitions in the containing state machine can have entry/exit points of the inserted state machine as targets/sources.
State in Protocol State machines
The states of protocol state machines are exposed to the users of their context classifiers. A protocol state represents an
exposed stable situation of its context classifier: When an instance of the classifier is not processing any operation, users
of this instance can always know its state configuration.
Attributes
Issue 9191 - add default values
• /isComposite : Boolean [1] A state with isComposite=true is said to be a composite state. A composite state is a state that contains at least one region. Default value is false.
• /isOrthogonal: Boolean [1] A state with isOrthogonal=true is said to be an orthogonal composite state. An orthogonal composite state contains two or more regions. Default value is false.
• /isSimple: Boolean [1] A state with isSimple=true is said to be a simple state. A simple state does not have any regions and it does not refer to any submachine state machine. Default value is true.
• /isSubmachineState: Boolean [1] A state with isSubmachineState=true is said to be a submachine state. Such a state refers to a state machine (submachine). Default value is false.
Associations
Package BehaviorStateMachines
Issue 8416 - add subsets constraint
• connection: ConnectionPointReference [0..*] The entry and exit connection points used in conjunction with this (submachine)
state, i.e., as targets and sources, respectively, in the region with the submachine state. A connection point reference references
the corresponding definition of a connection point pseudostate in the statemachine referenced by the submachinestate. {Subsets
Namespace ::ownedMember}
Issue 8433 - add subsets constraint and fix multiplicities to 0..*
• connectionPoint: Pseudostate [0..*] The entry and exit pseudostates of a composite state. These can only be entry or exit Pseudostates, and they must have different names. They can only be defined for composite states. {Subsets Namespace ::ownedMember}
• deferrableTrigger: Trigger [0..*] A list of triggers that are candidates to be retained by the state machine if they trigger no transitions out of the state (not consumed). A deferred trigger is retained until the state machine reaches a state configuration where it is no longer deferred.
Issue 8416 - add subsets constraints to doActivity, entry, exit
• doActivity: Behavior[0..1] An optional behavior that is executed while being in the state. The execution starts when this state is entered, and stops either by itself or when the state is exited whichever comes first. {Subsets Element::ownedElement}
• entry: Behavior[0..1] An optional behavior that is executed whenever this state is entered regardless of the transition taken to reach the state. If
defined, entry actions are always executed to completion prior to any internal behavior or transitions performed within the
state. {Subsets Element::ownedElement}
• exit: Behavior[0..1] An optional behavior that is executed whenever this state is exited regardless of which transition
was taken out of the state. If defined, exit actions are always executed to completion only after all internal activities
and transition actions have completed execution. {Subsets Element::ownedElement}
Issue 9094 -replace invalid redefines with subsets and multiplicity on ‘region’
• redefinedState: State[0..1] The state of which this state is a redefinition. {Subsets RedefinableElement ::redefinedElement}
• region: Region [0..*] {subsets ownedMember} The regions owned directly by the state.
• submachine: StateMachine[0..1] The state machine that is to be inserted in place of the (submachine) state.
• stateInvariant: Constraint [0..1] Specifies conditions that are always true when this state is the current state. In protocol state machines, state invariants are additional conditions to the preconditions of the outgoing transitions, and to the postcondition of the incoming transitions.
Issue 8416 -add redefines constraint
• /redefinitionContext: Classifier[1] References the classifier in which context this element may be redefined. {Redefines
RedefinableElement ::redefinitionContext}
Constraints
Issue 8416 -remove redundant constraint
[1] Only submachine states can have connection point references.
isSubmachineState implies connection->notEmpty ( )
[2] The connection point references used as destinations/sources of transitions associated with a submachine state must be
defined as entry/exit points in the submachine state machine.
Issue 8416 -add OCL expression
self.isSubmachineState implies (self.connection->forAll (cp | cp.entry->forAll (p | p.statemachine = self.submachine) and
cp.exit->forAll (p | p.statemachine = self.submachine)))
[3] A state is not allowed to have both a submachine and regions.
Issue 8416 -invert boldface
isComposite implies not isSubmachineState
Issue 8086 -Correct OCL.
[4] A simple state is a state without any regions.
isSimple = region.isEmpty()
Issue 8086 - Correct OCL.
[5] A composite state is a state with at least one region.
isComposite = region.notEmpty()
[6] An orthogonal state is a composite state with at least 2 regions.
isOrthogonal = (region->size () > 1)
[7] Only submachine states can have a reference statemachine.
isSubmachineState = submachine.notEmpty()
[8] The redefinition context of a state is the nearest containing statemachine.
redefinitionContext =
let sm = containingStateMachine() in
if sm.context->isEmpty() or sm.general->notEmpty() then
sm
else
sm.context
endif
[9] Only composite states can have entry or exit pseudostates defined.
connectionPoint->notEmpty() implies isComoposite
[10] Only entry or exit pseudostates can serve as connection points.
connectionPoint->forAll(cp|cp.kind = #entry or cp.kind = #exit)
Additional Operations
[1] The query isRedefinitionContextValid() specifies whether the redefinition contexts of a state are properly related to
the redefinition contexts of the specified state to allow this element to redefine the other. The containing region of a redefining
state must redefine the containing region of the redefined state.
[2] The query isConsistentWith() specifies that a redefining state is consistent with a redefined state provided that the
redefining state is an extension of the redefined state: A simple state can be redefined (extended) to become a composite
state (by adding a region) and a composite state can be redefined (extended) by adding regions and by adding vertices, states,
and transitions to inherited regions. All states may add or replace entry, exit, and doActivity actions.
[3] The query containingStateMachine() returns the state machine that contains the state either directly or transitively.
context State::containingStateMachine() : StateMachine
post: result = container.containingStateMachine()
Semantics
States in general
The following applies to states in general. Special semantics applies to composite states and submachine states.
Active states
A state can be active or inactive during execution. A state becomes active when it is entered as a result of some transition,
and becomes inactive if it is exited as a result of a transition. A state can be exited and entered as a result of the same
transition (e.g., self transition).
State entry and exit
Whenever a state is entered, it executes its entry behavior before any other action is executed. Conversely, whenever a state
is exited, it executes its exit behavior as the final step prior to leaving the state.
Behavior in state (do-activity)
The behavior represents the execution of a behavior, that occurs while the state machine is in the corresponding state. The
behavior starts executing upon entering the state, following the entry behavior. If the behavior completes while the state
is still active, it raises a completion event. In case where there is an outgoing completion transition (see below) the state
will be exited. Upon exit, the behavior is terminated before the exit behavior is executed. If the state is exited as a result
of the firing of an outgoing transition before the completion of the behavior, the behavior is aborted prior to its completion.
Deferred events
A state may specify a set of event types that may be deferred in that state. An event that does not trigger any transitions
in the current state, will not be dispatched if its type matches one of the types in the deferred event set of that state.
Instead, it remains in the event pool while another non-deferred event is dispatched instead. This situation persists until
a state is reached where either the event is no longer deferred or where the event triggers a transition.
State redefinition
A state may be redefined. A simple state can be redefined (extended) to become a composite state (by adding a region) and
a composite state can be redefined (extended) by adding regions and by adding vertices, states, entry/exit/do activities (if
the general state has none), and transitions to inherited regions. The redefinition of a state applies to the whole state
machine. For example, if a state list as part of the extended state machine includes a state that is redefined, then the state
list for the extension state machine includes the redefined state.
Composite state
Active state configurations
In a hierarchical state machine more than one state can be active at the same time. If the state machine is in a simple state
that is contained in a composite state, then all the composite states that either directly or transitively contain the simple
state are also active. Furthermore, since the state machine as a whole and some of the composite states in this hierarchy
may be orthogonal (i.e., containing regions), the current active state is actually represented by a set of trees of states
starting with the top-most states of the root regions down to the innermost active substate. We refer to such a state tree
as a state configuration.
Except during transition execution, the following invariants always apply to state configurations:
• If a composite state is active and not orthogonal, at most one of its substates is active.
• If the composite state is active and orthogonal, all of its regions are active, with at most one substate in each region.
Entering a non-orthogonal composite state
Upon entering a composite state, the following cases are differentiated:
• Default entry: Graphically, this is indicated by an incoming transition that terminates on the outside edge of the composite state. In this case, the default entry rule is applied (see Semantic variation point (default entry rule) ). If there is a guard on the trigger of the transition, it must be enabled (true). (A disabled initial transition is an ill-defined execution state and its handling is not defined.) The entry behavior of the composite state is executed before the behavior associated with the initial transition.
• Explicit entry: If the transition goes to a substate of the composite state, then that substate becomes active and its entry code is executed after the execution of the entry code of the composite state. This rule applies recursively if the transition terminates on a transitively nested substate.
• Shallow history entry: If the transition terminates on a shallow history pseudostate, the active substate becomes the most recently active substate prior to this entry, unless the most recently active substate is the final state or if this is the first entry into this state. In the latter two cases, the default history state is entered. This is the substate that is target of the transition originating from the history pseudostate. (If no such transition is specified, the situation is ill-defined and its handling is not defined.) If the active substate determined by history is a composite state, then it proceeds with its default entry.
• Deep history entry: The rule here is the same as for shallow history except that the rule is applied recursively to all levels in the active state configuration below this one.
• Entry point entry: If a transition enters a composite state through an entry point pseudostate, then the entry behavior is executed before the action associated with the internal transition emanating from the entry point.
Entering an orthogonal composite state
Whenever an orthogonal composite state is entered, each one of its orthogonal regions is also entered, either by default or
explicitly. If the transition terminates on the edge of the composite state, then all the regions are entered using default
entry. If the transition explicitly enters one or more regions (in case of a fork), these regions are entered explicitly and
the others by default.
Exiting non-orthogonal state
When exiting from a composite state, the active substate is exited recursively. This means that the exit activities are executed
in sequence starting with the innermost active state in the current state configuration.
If, in a composite state, the exit occurs through an exit point pseudostate the exit behavior of the state is executed after
the behavior associated with the transition incoming to the exit point.
Exiting an orthogonal state
When exiting from an orthogonal state, each of its regions is exited. After that, the exit activities of the state are executed.
Deferred events
Composite states introduce potential event deferral conflicts. Each of the substates may defer or consume an event, potentially
conflicting with the composite state (e.g., a substate defers an event while the composite state consumes it, or vice versa).
In case of a composite orthogonal state, substates of orthogonal regions may also introduce deferral conflicts. The conflict
resolution follows the triggering priorities, where nested states override enclosing states. In case of a conflict between
states in different orthogonal regions, a consumer state overrides a deferring state.
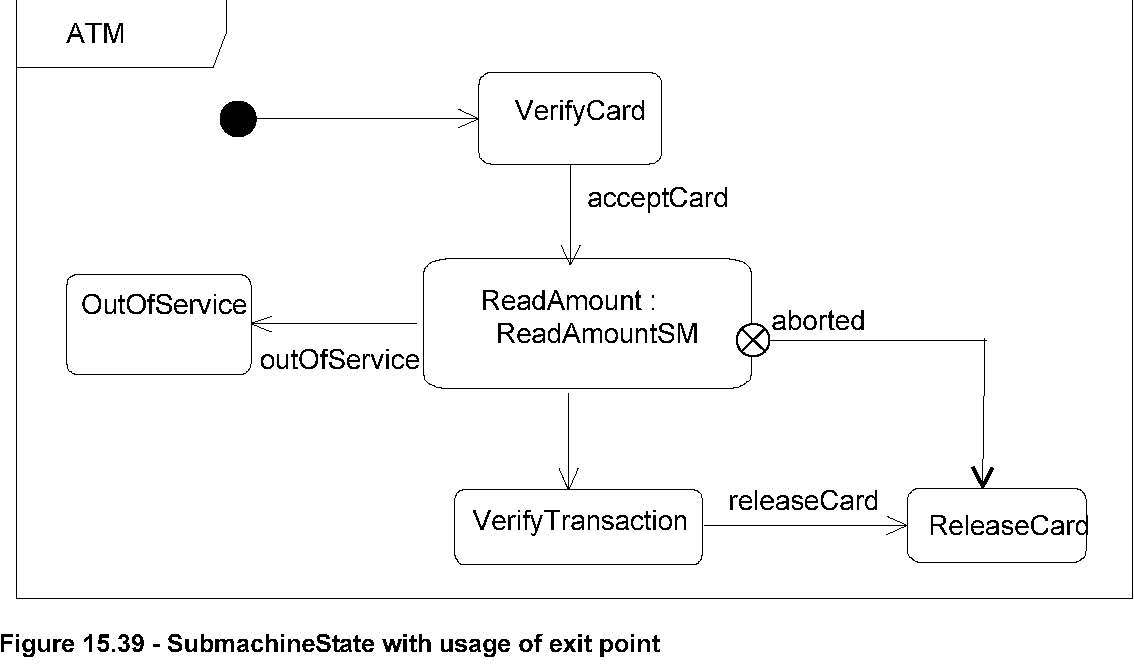
Submachine state
A submachine state is semantically equivalent to the composite state defined by the referenced state machine. Entering and
leaving this composite state is, in contrast to an ordinary composite state, via entry and exit points.
A submachine composite state machine can be entered via its default (initial) pseudostate or via any of its entry points (i.e.,
it may imply entering a non-orthogonal or an orthogonal composite state with regions). Entering via the initial pseudostate
has the same meaning as for ordinary composite states. An entry point is equivalent with a junction pseudostate (fork in case
the composite state is orthogonal): Entering via an entry point implies that the entry behavior of the composite state is
executed, followed by the (partial) transition(s) from the entry point to the target state(s) within the composite state.
As for default initial transitions, guards associated with the triggers of these entry point transitions must evaluate to
true in order for the specification not to be ill-formed.
Similarly, it can be exited as a result of reaching its final state, by a group transition that applies to all substates in
the submachine state composite state, or via any of its exit points. Exiting via a final state or by a group transition has
the same meaning as for ordinary composite states. An exit point is equivalent with a junction pseudostate (join in case the
composite state is orthogonal): Exiting via an exit point implies that first behavior of the transition with the exit point
as target is executed, followed by the exit behavior of the composite state.
Notation
States in general
A state is in general shown as a rectangle with rounded corners, with the state name shown inside the rectangle.
Ty ping
Password

Figure 15.30 - State
Optionally, it may have an attached name tab, see Figure 15.31. The name tab is a rectangle, usually resting on the outside
of the top side of a state and it contains the name of that state. It is normally used to keep the name of a composite state
that has orthogonal regions, but may be used in other cases as well. The state in Figure 15.25 on page 567 illustrates the
use of the name tab.

Figure 15.31 - State with name tab
A state may be subdivided into multiple compartments separated from
each other by a horizontal line, see Figure 15.32.
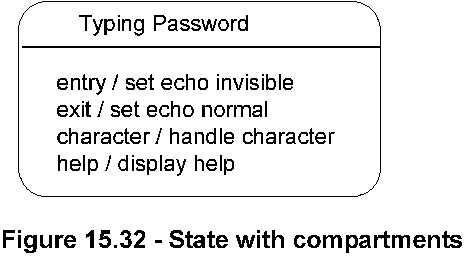
The compartments of a state are:
• name compartment
• internal activities compartment
• internal transitions compartment A composite state has in addition a
• decomposition compartment Each of these compartments is described below.
• Name compartment
This compartment holds the (optional) name of the state, as a string. States without names are anonymous and are all distinct.
It is undesirable to show the same named state twice in the same diagram, as confusion may ensue,
unless control icons (page 599) are used to show a transition oriented view of the state machine. Name
compartments should not be used if a name tab is used and vice versa.
In case of a submachine state, the name of the referenced state machine is shown as a string following ‘:’ after the name
of the state.
• Internal activities compartment
This compartment holds a list of internal actions or state (do) activities (behaviors) that are performed while the element
is in the state.
The activity label identifies the circumstances under which the behavior specified by the activity expression will be invoked.
The behavior expression may use any attributes and association ends that are in the scope of the owning entity. For list items
where the expression is empty, the backslash separator is optional.
A number of labels are reserved for various special purposes and, therefore, cannot be used as event names. The following
are the reserved activity labels and their meaning:
• entry — This label identifies a behavior, specified by the corresponding expression, which is performed upon entry to the state (entry behavior).
• exit — This label identifies a behavior, specified by the corresponding expression, that is performed upon exit from the state (exit behavior).
• do — This label identifies an ongoing behavior (do activity) that is performed as long as the modeled element is in the state or until the computation specified by the expression is completed (the latter may result in a completion event being generated).
• Internal transition compartment
This compartment contains a list of internal transitions, where each item has the form as described for Trigger.
Each event name may appear more than once per state if the guard conditions are different. The event parameters and the guard
conditions are optional. If the event has parameters, they can be used in the expression through the current event variable.
Composite state
• decomposition compartment
This compartment shows its composition structure in terms of regions, states, and transition. In addition to the (optional)
name and internal transition compartments, the state may have an additional compartment that contains a nested diagram. For
convenience and appearance, the text compartments may be shrunk horizontally within the graphic region.
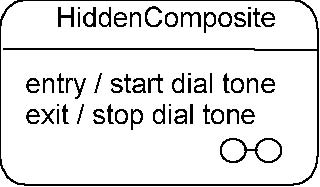
In some cases, it is convenient to hide the decomposition of a composite state. For example, there may be a large number of
states nested inside a composite state and they may simply not fit in the graphical space available for the diagram. In that
case, the composite state may be represented by a simple state graphic with a special composite icon, usually in the lower
right-hand corner (see
Figure 15.34). This icon, consisting of two horizontally placed and connected states, is an
optional visual cue that the state has a decomposition that is not shown in this particular state machine diagram. Instead,
the contents of the composite state are shown in a separate diagram. Note that the hiding here is purely a matter of graphical
convenience and has no semantic significance in terms of access restrictions.
A composite state may have one or more entry and exit points on its outside border or in close proximity of that border (inside
or outside).