Frequency Domain Analysis and Associated Demosaicking Algorithms for the Bayer Structure

This page reviews the theory for the Bayer structure and provides comprehensive results for the Kodak image dataset. It also adapts results and terminology (LSLCD) from the recent paper "Least-Squares Luma-Chroma Demultiplexing Algorithm for Bayer Demosaicking" to appear in IEEE Transactions on Image Processing.

Geometric structure of the Bayer color-filter array

The Bayer array pattern is regular and periodic and its geometric structure is the following:

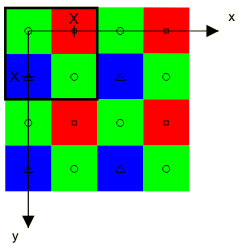
image of the Bayer structure

The Bayer sampling structure lies on an integer lattice Λ. The horizontal and vertical sampling spaces in this sampling structure are equal, the distance between them being X. X will be used as unit of length (pixel height, px).

The Bayer structure has three classes corresponding to the red (R), green (G) and blue (B) filters. The origin of the set is at the upper left corner with a green sample having a red sample to the right and a blue sample below. One period of the Bayer pattern determined by the sublattice Γ is indicated by the heavy square contour in the upper left corner.

Formation and representation of the Bayer CFA image

Following the chapter's theory and looking at the Bayer pattern above, one can come up with the following set of matrices:

Λ and Γ are the following two lattices:

The coset representatives of Γ in Λ are given by:

The matrix J defining the three input channels is given by:

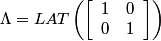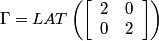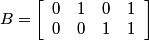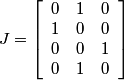Column 2 of the J matrix represents the green in the Bayer structure.

In the frequency domain, we have:

The reciprocal lattices Λ^* and Γ^* are:

The coset representatives for the set of cosets of Λ^* inΓ^* are given by:

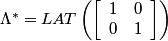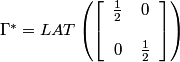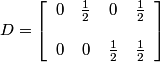The reciprocal lattices Λ^* (⊙) and Γ^* (+) and a suitable choice of representatives for the cosets of Λ^* in Γ^* are illustrated below:

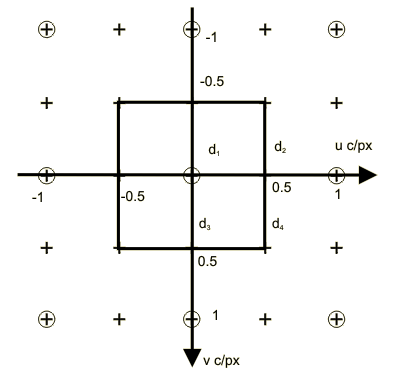
This gives:

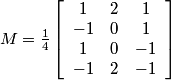The four transformed signals q_i are explicitly given by:

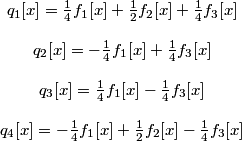Noting that q₃ = -q₂ the pseudo inverse matrix is given by:

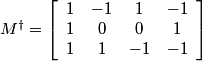This gives an inverse relationship that, considering the constraint q₃ = -q₂, simplifies to :

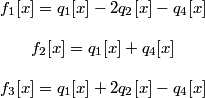Equations of thansformed signals. They can be read from M dagger .

In the frequency domain, the four transformed signals are modulated at the frequencies (0.0, 0.0), (0.5, 0.0), (0.0, 0.5) and (0.5, 0.5) so that:

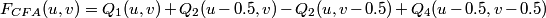The Bayer power density spectrum of an image will look similar to the one below. The frequency components q₁, q₂ and q₄ correspond respectively to the f_L, f_C2 and f_C1 components. Note that there are two separate independent copies of Q₂(u, v) at (0.5, 0.0) and (0.0, 0.5) respectively. On the figure these two different copies are marked as Q₂ and Q₃.

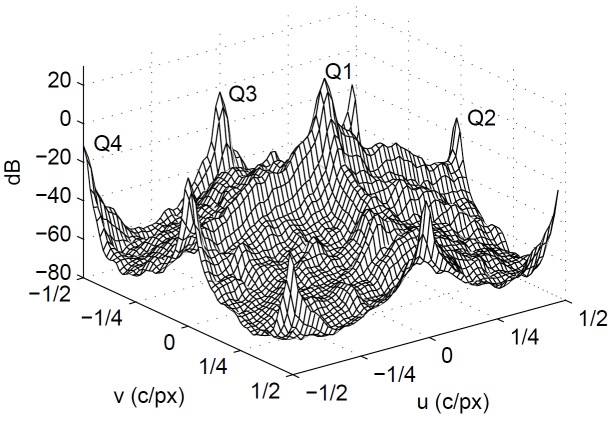
Power-specrtum when sampling following a Bayer structure

What is important to notice in this plot is that high frequency luma components overlap with high frequency chroma components. High frequency luma patterns intrude into the chrominance bands, resulting in false colors. High-frequency chrominance information intrudes into the luma band, resulting in false luma patterns, often having a zipper-like appearance.

Using C2a only using C2b only

The first image shows the demosaicking result when only the C2a component (Q₃) is used. The second image shows the demosaicking results when we use the C2b component (Q₂) of the spectrum exclusively.

Demosaicking algorithms derived from the frequency-domain representation using luma-chroma demultiplexing

The idea behind demosaicking algorithms based on the frequency-domain representation is to extract the luma and modulated chrominance components from the CFA signal using spatial filters and then to transform the demodulated chrominance components to the desired tristimulus values. In the process, the specific structure of the CFA signal should be exploited.

In the case of the Bayer sampling structure, one of the chroma components is modulated at two different frequencies: (0.5, 0.0) and (0.0, 0.5). Either one of these frequencies could be used to reconstruct the signal. However, if locally one suffers from crosstalk, the other one is relatively free of crosstalk. By adaptively selecting which of the two to use at each point, superior results are obtained.

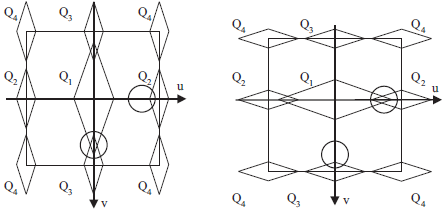
local spectrum scenarios schematically illlustrated for teh Bayer CFA pattern

The figures above illustrate schematically the local spectrum scenarios for the Bayer CFA. For the first scenario, Q₂ is the better estimate. For the second one, we would rather use Q₃.

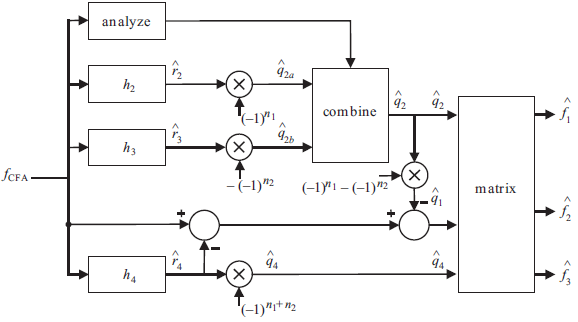
Adaptive demosaicking algotithm for the Bayer CFA

1. Filter f_CFA with a bandpass filter h₄ centered at frequency (0.5, 0.5) to extract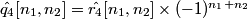

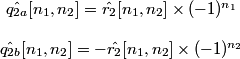and shift it to baseband to estimate :

2. Filter f_CFA with h₂ to get

and with h₃ to get

and, using q₂ = -q₃, demodulate to baseband:

3. The local average energies e_X and e_Y are estimated using modulated Gaussian filters with standard deviations of r_G1 and r_G2 px along major and minor axes, centered at frequencies (±u_m, 0.0) and (0.0, ±v_m) c/px respectively. The filter at (0.0, ±v_m) is the transpose of the filter at (±u_m, 0.0). This is followed by smoothing of the squared output with a 5 by 5 moving average filter.

4. Using the coefficinet w = e_Y / (e_X + e_Y), the estimate of q₂ is obtained as:

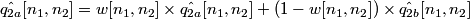5. The luma component is estimated by:

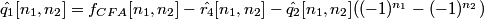6. Estimate RGB components from and .

The block diagram of adaptive demosaicking algorithm for the Bayer CFA structure is below:

Least-squares filter design for CFA signal demultiplexing

The filter design method is a crucial step for successful implementation of demosaicking algorithms. The method used to design these filters: Least Squares Luma Chroma Demultiplexing (LSLCD) has been explained in the book chapter (but not under that name). Assuming that the difference between the original image and its demultiplexed variant can be modeled as a stationary random field, the filters are designed such that they minimize the expected square error:

In practice, the original image is not available. The estimation error is minimised using a training set. In our experiments, the training set was one of the following:

the image itself (not implementable, but gives a bound on possible performance for that image),
the first 12 images of the Kodak set,
the other 23 images of the kodak set or
all the 24 images of the Kodak set

For the Bayer pattern, the approach needs to be used to determine the three filters h₂, h₃ and h₄. Beause h₂ and h₃ are both representatives of the chroma 2 component the least squares algorithm needs to be done simultaneously on both in order to minimize the squared error estimation of q₂ (the procedure used to take both chroma components in consideration is explained above). The estimate of q₂[n₁, n₂] then becomes:

h₂ and h₃ can be chosen jointly to minimize the total squared error between q₂ and over the training set. We cast this squared error in matrix form. Let h₂₃ be the 2N_B x 1 column vector obtained by stacking h₂ on top of h₃. The column vector q⁽ⁱ⁾₂ is obtained by scanning the elements of q₂[n₁, n₂] over W ⁽ⁱ⁾. Finally, we form a N_W x 2N_B matrix W⁽ⁱ⁾ as follows: the first N_B columns are formed by reshaping w⁽ⁱ⁾[n₁, n₂](-1)^n₁ f ⁽ⁱ⁾_CFA[n₁-k₁, n₂-k₂] for each (k₁, k₂) ∈S while the second N_B columns are formed by reshaping -(1-w⁽ⁱ⁾[n₁, n₂])(-1)^n₂ f ⁽ⁱ⁾_CFA[n₁-k₁, n₂-k₂] in the same order. This leads to a least squares problem of the form:

Finally, h₂ and h₃ are extracted from h₂₃ and reshaped to give the optimised filters h₂[x] and h₃[x].

An example the frequency response of the filters obtained using this procedure can be found here.

The recommended values for the various parameters and regions of support are:

for step 3 of the algorithm u_m = v_m = 0.375 c/px, r_G1 = 3.0, r_G2 = 1.0 and a maximum support for the Gaussian filters of 11x3
filters h₂, h₃ and h₄ have a maximum support 11x11

Least-squares luma-chroma demultiplexing (LSLCD) algorithm results

A full list of results for the 24 Kodak images can be found here.

The table below shows the LSLCD algorithm results for the first 3 Kodak images. The training sets are chosen as follows:

Column A: LSLCD with ST filter (configuration [11 11 11 11 11 11], obtained by self-training on the given image)
Column B: LSLCD with TO filter (configuration [11 11 11 11 11 11], obtained by training on other 23 images)
Column C: LSLCD with RE filter (configuration [5 5 9 3 11 1], obtained by training on other 23 images)
Column D: LSLCD with RE filter (configuration [5 5 9 3 11 1], obtained by self-training on the given image)

No.	Thumb	Original	A	B	C	D
1		TIFF JPG	TIFF JPG 39.55 1.052	TIFF JPG 38.67 1.133	TIFF JPG 38.17 1.193	TIFF JPG 37.92 1.190
2		TIFF JPG	TIFF JPG 41.54 0.581	TIFF JPG 40.81 0.642	TIFF JPG 40.84 0.628	TIFF JPG 40.65 0.664
3		TIFF JPG	TIFF JPG 43.22 0.481	TIFF JPG 43.37 0.509	TIFF JPG 42.76 0.490	TIFF JPG 42.22 0.512

LSLCD optimization - quality vs complexity

The details of the complexity analysis can be found here. The quality versus complexity plots are presented below.

CMSE versus complexity plot

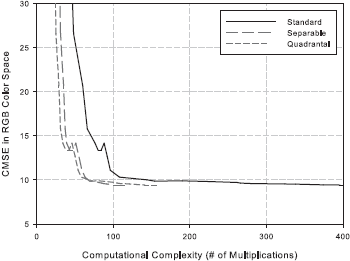
CMSE vs complexity plot

S-CIELAB versus complexity plot

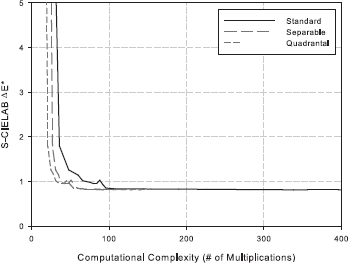
S-cielab vs complexity plot

Following the analysis, we identify the configuration [ 5 5 9 3 11 1 ] as a good choice. This corresponds to a 5 x 5 least-squares filter h₄, 9 x 3 least-squares filter h₂, 3 x 9 least-squares filter h₃, 11 x 1 Gaussian filter h_G1 centered at (0.375, 0.0) c/px, and 11 x 1 Gaussian filter h_G2 centered at (0.0, 0.375) c/px.

Software download

The results presented are reproducible. Bayer_lslcd.zip provides the necessary code to do so. The MATLAB files that are included should be run separately when results are reproduced.

LSLCD algorithm computations: Bayer_lslcd.zip

Metrics: CMSE_S-CIELAB calculators.