The results reported on the numbers and sizes of large sublattices of 
would not have been obtained without a heavy dose of experimental mathematics
preceding the theoretical analysis. Also, one may wonder why just the
P(0,2,3,n;n) are the chosen ones among all the layer cakes available. These
questions are addressed in [44] whose core is the classification of all
5505 proper maximal sublattices of 
(with 37 elements) into
isomorphism types and which provided the clues for the classification of all
large sublattices of the lattices for all n. Nüssli's Masters
Thesis
relies on a bunch of C 
programs designed to generate maximal sublattices
of 
. They give acceptable running times for 
on a
SUN-workstation, but for 
the situation becomes more difficult (mainly
due to storing and listing problems).
Apart from the more heuristic considerations reported in 3.1 which led to layer cake lattices, their outstanding feature - from the computational point of view - is that they are lattices of sets and that join and meet are basically set union and intersection. Since such operations are very fast in most programming languages, we obtain good running times even for brute force algorithms.
So why levels 2 and 3? The attractive feature here is the easy graphical representation of sublattices of any L(X): If S is such a sublattice, represent it as a graph G(S) with vertex set X and with all 2-sets of S as edges; there is no need to display 3-sets of S which arise as joins of 2-sets (these are given by adjacent pairs of edges of G(S)), so only the join-irreducible 3-sets must be marked additionally. The effect of the quadrangle argument used so heavily in subsection 3.2 then reduces to adding the diagonals to a 4-cycle in G(S).
We illustrate this by an example. What is the number of elements it takes to
generate for 
? Looking for generating sets consisting of
2-sets exclusively, the following pictures provide an answer:
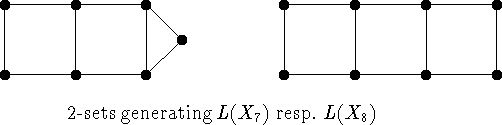
Denote by g(n) the least number of 2-sets needed to generate . It is
not hard to see from the figure that 
and that 
.
We think that these bounds are sharp but have not proved it. So the problem of
determining the size of minimal generating sets of is open, as well as
some related questions: E.g., given a generating set 
, is it
possible to find a generating set 
(resp. 
) consisting of 2-sets
(resp. 3-sets) exclusively such that 
(resp. 
)?