References

1

M. E. Adams, Ph. Dwinger and J. Schmid, Maximal sublattices of finite distributive lattices, preprint, 1995

2

M. E. Adams, R. Freese, J. B. Nation and J. Schmid, Maximal sublattices and Frattini sublattices of bounded lattices, preprint, 1995

3

M. Aigner, Lexicographic matching in Boolean algebras, J. Comb. Theory Series B 14 (1973), 187 - 194

4

G. Birkhoff, Lattice Theory, Amer. Math. Soc. Colloq. Publ. Vol. 25, Providence, R. I., 1967

5

G. R. Brightwell, H. A. Kierstead, A. V. Kostochka and W. T. Trotter, The dimension of suborders of Boolean lattices, Order 11 (1994), 127 - 134

6

G. R. Brightwell, H. J. Prömel and A. Steger, The average number of linear extensions of a partial order, J. Comb. Theory Ser. A 73 (1996), 193 - 206

7

G. Burosh and J. Laborde, Einbettungen von Graphen in den n-Würfel, in: K. Wagner and H. Bodendiek (eds.), Graphentheorie III, BI Wissenschaftsverlag, 1992, 73 - 94

8

Betty Crocker, Cookbook, 21 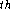printing, Golden Press, New York, 1974, p. 92 and p. 125

9

I. J. Dejter, Hamilton cycles and quotients of bipartite graphs, in: Y. Alavi et al. (eds.), Proc. Vth Imternat. Conf. Theory Appl. Graphs, Wiley, New York, 1985, 189 - 199

10

I. J. Dejter,W. Cedeño and V. Jauregui, A note on Frucht diagrams, Boolean graphs and Hamilton cycles, Discrete Math. 114 (1993), 131 - 135

11

I. J. Dejter, J. Córdova and J. Quintana, Two Hamilton cycles in bipartite reflective Kneser graphs, Discrete Math. 72 (1988), 63 - 70

12

D. Z. Djokovič, Distance preserving subgraphs of hypercubes, J. Comb. Theory Ser. B 14 (1973), 263 - 267

13

D. Duffus, P. Hanlon and R. Roth, Matchings and Hamiltonian cycles in some families of symmetric graphs, Emory University Technical Report, 1986

14

D. Duffus, H. A. Kierstead and H. S. Snevily, An explicit 1-factorization in the middle of the Boolean lattice, J. Comb. Theory Series A 65 (1994), 334 - 342

15

D. Duffus, V. Rödl, B. Sands and R. Woodrow, Enumeration of order-preserving maps, Order 9 (1992), 15 - 29

16

D. Duffus, B. Sands and P. Winkler, Maximal chains and antichains in Boolean lattices, SIAM J. Discrete Math. 3 (1990), 197 - 205

17

D. Duffus, B. Sands and R. Woodrow, Lexicographic matchings cannot form Hamiltonian cycles, Order 5 (1988), 149 - 161

18

B. Dushnik, Concerning a certain set of arrangements, Proc. Amer. Math. Soc. 1 (1950), 788 - 796

19

B. Dushnik and E. W. Miller, Partially ordered sets, Amer. J. Math. 63 (1941), 600 - 610

20

J. D. Farley, The number of order presrving maps between fences and crowns, Order 12 (1995), 5 - 44

21

Z. Füredi, The order dimension of two levels of the Boolean lattice, Order 11 (1994), 15 - 28

22

Z. Füredi, P. Hajnal, V. Rödl and W. T. Trotter, Interval orders and shift graphs, in: A. Hajnal and V. Sos (eds.), Sets, graphs and numbers, Proc. Colloq. Math. Soc. Janos Bolyai, vol. 60, Budapest, Hungary, 1991, 297 - 313

23

Z. Füredi and J. Kahn, On the dimensions of ordered sets of bounded degree, Order 3 (1986), 17 - 20

24

Z. Füredi and K. Reuter, The jump number of suborders of the power set order, Order 6 (1989), 101 - 103

25

G. Gierz, Level sets in finite distributive lattices of breadth 3, Discrete Math. 132 (1994), 51 - 63

26

G. Gierz and F. Hergert, The bandwidth problem for distributive lattices of breadth 3, Discrete Math. 88 (1991), 157 - 177

27

G. Havas and M. Ward, Lattices with sublattices of a given order, J. Comb. Theory 7 (1969), 281 - 282

28

I. Havel, Semipaths in directed cubes, in: M. Fiedler (ed.), Graphs and other combimatorial topics, Teubner, Leipzig, 1983, 101 - 108

29

I. Havel and J. Movárek, B-valuations of graphs, Czech. Math. Journal 22 (1972), 338 - 351

30

F. Harary, J. P. Hayes and H.-J. Wu, A survey of the theory of hypercube graphs, Comput. Math. Appl. 15 (1988), 277 - 289

31

J. Hashimoto, Ideal theory for lattices, Math. Japon. 2 (1952), 149 - 186

32

G. H. Hurlbert, A. V. Kostochka and L. A. Talysheva, The dimension of interior levels of the Boolean lattice, Order 11 (1994), 29 - 40

33

H. A. Kierstead, On the order dimension of 1-sets versus k-sets, J. Comb. Theory Ser. A 73 (1996), 219 - 228

34

H. A. Kierstead and W. T. Trotter, Explicit matchings in the middle levels of the Boolean lattice, Order 5 (1988), 163 -171

35

D. J. Kleitman and B. L. Rothschild, Asymptotic enumeration of partial orders on a finite set, Trans. Amer. Math. Soc. 205 (1975), 205 - 220

36

A. D. Korshunov, on the number of monotone Boolean functions, Probl. Kibern. 38 (1981), 5 - 108 (in Russian)

37

D. W. Krumme, K. N. Venkataraman and G. Cybenko, Hypercube embedding is NP-complete, in: M. T. Heath (ed.), Proc. 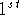Conf. on Hypercube Multiprocessors, SIAM, Philadelphia, 1986, 148 - 157

38

L. Lippert, Automorphismen Boole'scher Schichtenkuchen, Masters Thesis, University of Bern, in preparation

39

W.-P. Liu, I. Rival and N. Zaguja, Automorphisms, isotone self-maps and cycle-free orders, Discrete Math. 144 (1995), 59 - 66

40

W.-P. Liu and H. Wan, Automorphisms and isotone self-maps of ordered sets with top and bottom, Order 10 (1993), 105 - 110

41

Z. Lonc, Partitions of large Boolean lattices, Discrete Math. 131 (1994), 173 - 181

42

J. Mitas and K. Reuter, Cover-preserving embeddings of bipartite orders into Boolean lattices, Theor. Comput. Sci., to appear

43

J. Mitas and K. Reuter, Subgraphs of hypercubes and subdiagrams of Boolean lattices, preprint, December 1995

44

M. Nüssli, Maximale Unterverbände Boole'scher Schichtenkuchen, Master's Thesis, University of Bern, 1996 (unpublished)

45

I. Rival and A. Rutkowski, Does almost every isotone self-map have a fixed point?, in: Extremal problems for finite sets, Bolyai Soc. Math. Studies 3 (Visegrad, Hungary, 1991), 413 - 422

46

J. Spencer, Mimimal scrambling sets of simple orders, Acta Math. Acad. Sci. Hung. 22 (1971), 349 - 353

47

W. T.Trotter, Some combinatorial problems for permutations, Congressus Numerantium 19 (1978), 179 - 191

48

W. T. Trotter, Combinatorics and partially ordered sets: Dimension theory, John Hopkins Univ. Press, Baltimore and London, 1992

49

M. Wild, Cover-preserving order embeddings into Boolean lattices, Order 9 (1992), 209 - 232

50

N. Zaguia, Isotone maps: Enumeration and structure, in: N. W. Sauer, R. E. Woodrow and B. Sands (eds.), Finite and infinite combinatorics in sets and logic, NATO ASI Series, Series C: Math. and Phys. Sci. Vol. 411, Kluwer Acad. Publ., Dordrecht, 1993, 421 - 430