Large sublattices of Boolean layer cakes: Types

 

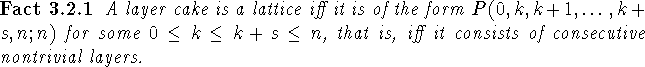
Some Boolean layer cakes are lattices under their induced order. Indeed, we have the following

 

Proof: Suppose P is realized on X and contains layers k and k+s (0<k<k+s<n, ) but none of the layers j with k<j<k+s. Pick a j-set and write it as the union of k-sets . has no least upper bound within P since any two k+s-sets containing Y provide incomparable minimal upper bounds.

For the remainder of this paper, we will deal almost exclusively with layer cakes consisting of levels 0,2,3,n. We introduce the following conventions to smoothen the presentation:

We use as a shorthand for the lattice P(0,2,3,n;n). Since we will be dealing with different realizations of at the same time, we adopt the following abbreviations: Given any (finite) set X with , T(X) stands for the the ordered set of all 2-subsets and all 3-subsets of X, and L(X) for the lattice obtained from T(X) by adjoining top and bottom. Sublattice will always mean 0-1-sublattice, so L(Y) is a sublattice of L(X) whenever . will denote a set with n elements, hence . For , let .

We call a sublattice S of large iff its size exeeds that of the next smaller layer cake of the type considered here, that is, if . The purpose of this subsection is to classify all large sublattices of and to show that they all contain a copy of as a sublattice (Theorem 3.2.11).

Let S be any sublattice of L(X). Define , and . Also, , and . Thus |S| = d(S)+2.

Further, an S-quadrangle is any set of four distinct points such that , , and all belong to S. The basic fact about S-quadrangles is

 

Proof: by the arithmetic of L(X), and analogously for . The four 3-subsets of must be in S as least upper bounds of 2-subsets.

 

Proof: Let and define similarly. Assume n=2k. If , then and analogously for . It follows that , so pick two points in . But then is an S-quadrangle and by 3.2.2 we have as claimed. The proof for the case n=2k+1 is similar.

The main consequence of Lemma 3.2.3 is the existence of points with low value of whenever S is a proper sublattice of L(X).

 

Proof: Assume n=2k and suppose for all . By 3.2.3 S must then contain all 2-subsets of and so . The proof for n=2k+1 is analogous.

The bounds k-1 respectively k provided by 3.2.4 are sharp in the following sense: There exist proper sublattices such that for all (if n=2k) respectively for all (if n=2k+1). Indeed, let with |Y|=|Z| and (if n=2k) respectively (if n=2k+1) and let S be together with top and bottom.

The following lemma relates the values of and :

 

Proof: If w=0, any two 3-subsets of containing p must be disjoint within , for otherwise their meet would be a 2-set containing p. Their number is thus at most [(n-1)/2]. Suppose and let . There are 3-sets with and . Every point can belong to at most one 3-set containing p, since otherwise would arise as meet. So there are at most n-w-1 such 3-sets not contained in (this number being actually attained for suitable S).

Combining 3.2.4 and 3.2.5, we obtain

 

Proof: Define . g is monotonic in u for .

Suppose n=2k. Since , we have . Choose as provided by 3.2.4. By 3.2.4, we infer . If , monotonicity of g and 3.2.5 imply , thus as desired. If w=0, by 3.2.5(ii), thus . If w=1, by 3.2.5(i), thus . Now , so the desired inequality holds also for w=0,1.

Suppose n=2k+1. Since , we have . Choose as provided by 3.2.4. By 3.2.4, we infer . For , proceed as above. For w=0, we have , thus . If w=1, we obtain , thus . Now , giving the desired inequality also for w=0,1.

For a given sublattice S of L(X) and any point , we define together with top and bottom. S[p] is a sublattice of L(X), the p-trace of S. 3.2.6 implies that any proper sublattice has some relatively big p-traces:

 

Proof: |S[p]|=|S|-d(S,p).

The following proposition provides the base for the inductive proof of the classification theorem 3.2.11:

 

Proof: If , then . So assume S is a proper sublattice and choose as provided by 3.2.7. We must show that implies . Now |S[p]|=|S|-d(S,p), so we are done if we can show that . By direct calculation, .

Assume first n=2k, thus . Now by 3.2.6(i), so the desired inequality boils down to . Replacing n by 2k, this is seen to hold provided , which in turn is true iff , a condition satisfied in our case.

Assume now n=2k+1, thus . In this case by 3.2.6(ii), so must be shown. Replacing n by 2k+1, this is equivalent to , which is true whenever , satisfied in our case.

We will be concerned with the following particular sublattices of L(X) in the sequel:

Choose two distinct points p and q in X. S(X,p,q) is the sublattice with elements together with top and bottom.

Let be any nonempty collection of pairwise disjoint 2-subsets of . is the sublattice with elements together with top and bottom.

It is easy to see that and , so all these lattices are large.

 

Proof: Suppose . Any 2-subset of X belonging to S but not to S(X,p,q) must be of the form with . If there is any , y different from p,q,x, then is an S-quadrangle and thus . In any case, S contains all 2-subsets of X, contradicting S proper. Hence S contains no 2-sets outside S(X,p,q). Suppose there is a 3-set in S but not in S(X,p.q), necessarily of the form with x,y both different from q. But then would be a 2-set in S but not in S(X,p,q) which we just saw is impossible. We conclude that S=S(X,p,q).

Let now and assume that . Then and thus S=S(X,p,q) as S is proper, by the first half of this proof. So we may assume that consists exclusively of 3-sets, necessarily of the form . Any two 3-sets in S must be disjoint within for otherwise their meet would produce a 2-set in , contrary to assumption. We conclude that for some collection .

 

We are now ready to state the main theorem of this subsection:

 

Proof: We use induction on n and thus assume that and the theorem holds for all n' with . Let S be a proper large sublattice of and use Prop. 3.2.8 to choose a point such that S[p] is large in . All lattices under consideration will be regarded as sublattices of . There are three cases: S[p] may be (i) itself, or (ii) for some in , or (iii) for some and collection of pairwise disjoint subsets of .

(i) is easy; If , consists of 3-sets exclusively which must be disjoint within , and thus for some . If , then for some . Since S is proper, we infer by Corollary 3.2.10.

For (ii), we first show that is not possible. Indeed, if , then by 3.2.5 and thus . Now , whence . We will show that , a contradiction since S is large. The required inequality is equivalent to . Now and our inequality reduces to which is satisfied whenever . We conclude that . Hence there are in such that and belong to S. It follows that for any further , the set is an S-quadrangle and thus . Consequently, and thus as in (i).

For (iii), observe that , so the same argument as in (ii) shows that . Also the same quadrangle argument applies and shows that S includes every 2-set and 3-set contained in . Since is nonempty, we find , x,y both different from p,q. This excludes the possibility that for otherwise , say, and thus , a contradiction. Consequently, , finishing the inductive step of the proof of 3.2.11.

It remains to show that 3.2.11 is true for n=6. Assume S is a proper large sublattice of , thus . By 3.2.6 we find such that and . Working within , we find such that and . It follows that . Now if , then by 3.2.5 and thus . But this would imply that , contradicting . Hence and by the usual quadrangle argument we obtain that . If , then we must have by 3.2.5 in order to obtain . It follows that with . If , then S includes for some and so equals by 3.2.10 as S is proper.