Syntax analysis

Course notes for Section 2, Chapter 3 of the course SEG 2106
by Gregor v. Bochmann, February 2004 (translated to English: January 2008, revised 2009, 2010, 2011, 2012, 2013, 2015)

Recursive language equations

Recursive equations

You know recursive equations from linear algebra. Example:

• x1 = a11 * x1 + a12 * x2 + b1
• x2 = a21 * x1 + a22 * x2 + b2

These are equations over the field of real numbers where multiplication has an inverse, the division. Therefore we can find a solution by substitution. For instance, we obtain from the first equation the following expression for x1 : x1 = 1/(1-a11) * (a21 * x2 + b1). This can be substituted into the second equation which then can be solved for x2.

The inverse operation does not exist for the union and concatenation operators that are used for equations among strings (e.g. regular expressions). Therefore such a method cannot be used for solving a system of language equations.

There exists another method for solving a system of recursive equations (which, however, does not work in all situations). This is finding a solution by interative substitution starting with some dummy initial values for all variables. Here is an example: We consider the (single) recursive equation x = 0.5 * x + 4. We write x(i) for the i-th value of x obtained in the i-th iteration. If we assume the initial value of x to be x(0) = 0.0, then we get the following sequence of values for x, where x(i) is substituted in the equation to obtain the value x(i+1). Here we go: x(0) = 0.0; x(1) = 4.0; x(2) = 6.0; x(3) = 7.0; x(4) = 7.5; etc. We see that we never reach the exact solution, which is x = 8.0, but we approach this value arbitrary closely by continuing the iterations. One says that the value of v(i) converges to the solution, as i goes to infinity (as you have heard in your mathematics courses).

Recursive language equations

Now we consider recursive equations between formal languages, that is, the variables that we consider have values that are languages, that is, sets of strings over a given alphabet - as discussed at the beginning of the chapter on lexical analysis. As discussed there, a system of language equation is normally called a grammar. We define here these equations using the set notation which was used in the previous chapter for Formal Languages. Please note, that one could also use the BNF notation which is normally used for defining grammars.

As an example, we consider here the alphabet A = {a, b, c}. The languages over A are the subsets of A* (the set of all sequences formed from elements in A). As in the discussion of regular languages, we use the operators union (U), and concatenation (.) applied to languages (sets of sequences over the alphabet) in order to define new languages.The following definitions of various complexity.

Example 1: Here are two examples of (non-recursive) language equations (finite languages defined by enumeration). Note, this corresponds to equations of the form "x = 3.2" in the case of equations for real numbers.

• L1 = {a, b, bb}

• L2 = {ε, aa, cba}

Example 2 - with fix-point solution : Here is a system of three recursive equations (without the use of the concatenation operator):

• L9 = {c} U   L10
• L10 =  L9  U  {a}
• L11 =  L9  U  {a, b}

This system can be solved by iterative substitution as follows.

• L9⁽⁰⁾ = L10⁽⁰⁾ = L11⁽⁰⁾ = Ø  (initial values)

• L9⁽¹⁾ = {c};   L10⁽¹⁾ = {a} ; L11⁽¹⁾ = {a, b}  (first iteration)
• L9⁽²⁾ = {a, c};   L10⁽²⁾ = {a, c} ; L11⁽²⁾ = {a, b, c}    (second iteration)
• L9⁽³⁾ = {a, c};   L10⁽³⁾ = {a, c} ; L11⁽¹⁾ = {a, b, c}    (third iteration, and all subsequent iterations); we have reached what is called a fix point.
  

Note: For any system of language equation not using the concatenation operator, there is always a finite fix point solution. Why ?? - We will find these kind of equations with fix-point solutions when we calculate the set First and Follow for LL(1) grammars (see below)

Regular languages

Example 3: A regular definition is a system of equations where the right side of each equation is a regular expression without recursiveness. The following example is specially simple because it does not use the star operator:

• L1 = {a, b, bb}

• L2 = {ε, aa, cba}
• L3 = L1 . L2   U  {aa, bb}

Note: A regular definition can be solved by substitution. In the case of this example, we obtain for L3:

L3 = ( {a, b, bb} . {ε, aa, cba}) U  {aa, bb}

Example 4 - left recusion: A (single) left-recursive equation (left recursion means that the recursive variable is on the left side of a concatenation):

• L4 = {a} U  L4 . {b}

This equation can be solved by iterative substitution, as follows:

• L4⁽⁰⁾ = Ø  (initial value)

• L4⁽¹⁾ = {a}  (first iteration)
• L4⁽²⁾ = {a, ab}  (second iteration)
• L4⁽³⁾ = {a, ab, abb}  (third iteration)
• etc. - this continues and L4 will include eventually all sequences consisting of "a" followed by n consecutive "b", for any positive number n.
• In this case, there is no fixed point reached after a finite number of iterations, but the value of L4 obtained at each iteration becomes more close to the fixed point which is the infinite set of sequences that can be written using Kleene's star operator as follows: "{a} ({b})* ", or as the regular expression " a b* " .
• Conclusion: The solution of a (single) left-recursive equation is a regular language that can be defined by a regular expression.

A more general equation is the following: LG = L1 U LG . L2 where L1 and L2 are finite languages, for instance those defined above. By iterative substitution, we obtain:

• LG⁽⁰⁾ = Ø  (initial value)

• LG⁽¹⁾ = L1  (first iteration)
• LG⁽²⁾ = L1 U L1 . L2 = L1 . ({ε} U L2) - (second iteration)
• LG⁽³⁾ = L1 U L1 . L2 U L1 . L2 . L2 = L1 . ({ε} U L2 U L2.L2) -  (third iteration)
• etc. - this continues and LG will include eventually all sequences consisting of n times some element of L2, for any positive number n, preceeded by some element of L1. Note: The solution can also be written using the Kleene operator as LG = L1 . L2 * .

Alternative definitions of Kleene's star operator

Let us consider the language equation above: LG = L1 U LG . L2 , and assume that L1 = {ε}, then we see that the solution to this equation is L2*. This can be taken as an alternative definition of Kleene's star operator: " L2* is the solution to the equation LG = {ε} U LG . L2 ".

It is interesting to note that the equation LG = {ε} U  L2 . LG has the same solution. This is a right-recursive equation.

Therefore we can conclude that the two grammars

are equivalent - define the same language LG. This will be useful for the elimination of left recursion which we need to perform for LL(1) parsing - as discussed later in this chapter.

Non-regular languages

Example 5: Here is another example:

• L5 = {c} U  {a}. L5 . {b}

We can develop the solution by iterative substitution as follows:

• L5⁽⁰⁾ = Ø  (initial value)

• L5⁽¹⁾ = {c}   (first iteration)
• L5⁽²⁾ = {c, acb}   - (second iteration)
• L5⁽³⁾ = {c, acb, aacbb} -  (third iteration) , etc.

We see that the fixed point of this equation consists of all strings that have a certain number of a, then one c followed by the same number of b (as there were a's at the beginning). Sometimes one writes " aⁿ.c.bⁿ ".

It is important to note that there exists no accepting automaton that is able to accept exactly this language, because during the initial sequence of a's, the automaton has to count the number of a's, each additional a corresponds to a new state of the automaton. Since there is no limit on the number of a's that may be there before the c, the number of states of the automaton cannot be finite. Therefore, only a automaton with an infinite number of states could do the job, but that would not be a finite state machine. Conclusion: This language is not regular (i.e. there is no regular expression that can define this language)

Some more examples

(1) Discuss some examples of "garden grammars"

(2) Each system of language equations is a grammar. Note: the alphabet is A = {a, b, c, d}

Syntax trees and the meaning of programs

An example: Arithmetic expressions

We consider here several grammars for simplified versions of arithmetic expressions, such as " 3 + a * ( b -5) ".

The simplest grammar appears to be the following Grammar-E1:

• E -> C | V | E "+" E | E "-" E | E "*" E | "(" E ")"
• C -> integer
• V -> identifier

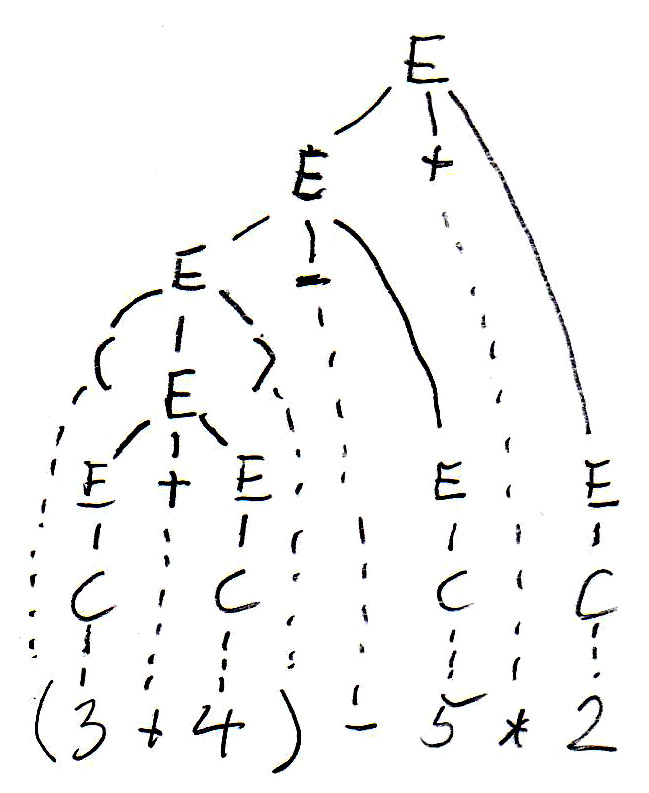
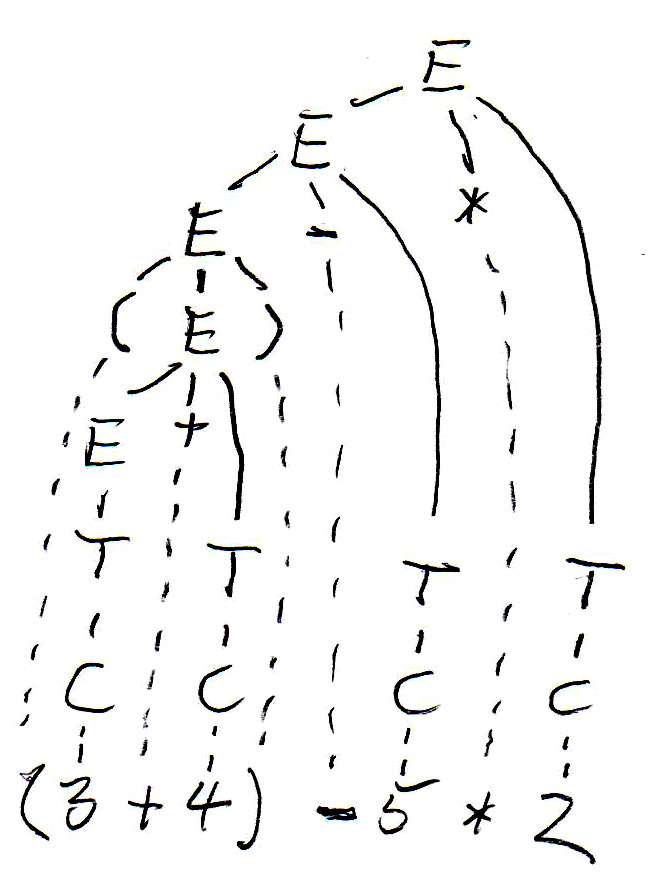
For the expression " (3 + 4) - 5 * 2 ", this grammar gives rise to two different syntax trees as follows:

The syntax tree guides the evaluation of the expression (which is the meaning of an expression - we want to know what the value of the expression is). Subexpressions within parenthesis must be evaluated first - this gives rise to bottom-up evaluation over the syntax tree.

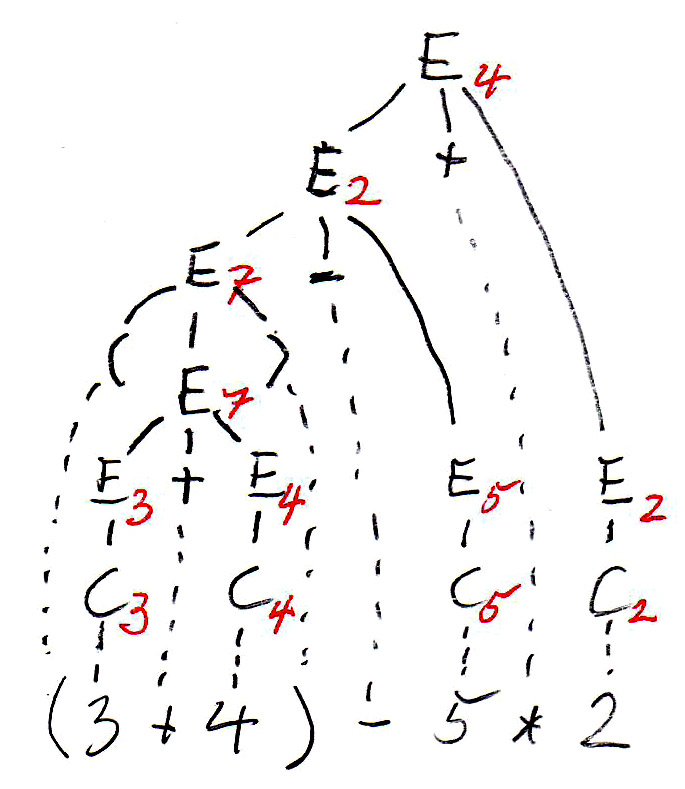
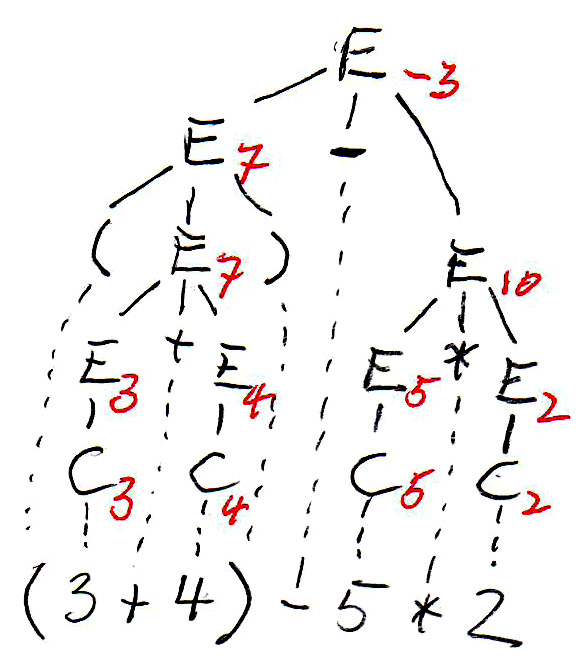
In the syntax trees are copied below, and the non-terminal symbols of the tree (which represent subexpressions) are annotated with their values. We see that the two trees define different values for the same expression. This is because the left tree corresponds to left-to-right evaluation (which is the common way of evaluating expressions), while the right tree corresponds to right-to-left evaluation. We see that this grammar is ambiguous since it gives rise to two different meanings (semantics) for the same expression (sentence). In order to avoid this problem, we have to find an equivalent grammar for expressions that is not ambiguous.

Ambiguity and equivalence (some definitions)

Equivalence: Two grammars are equivalent if they generate the same language. (Already seen earlier)

Ambiguous sentence: A sentence is ambiguous if the syntax rules allow the construction of two different syntax tree for the given sentence.

Ambiguous grammar: A context-free grammar is ambiguous if there exists a sentence accepted by the syntax that is ambiguous.

Coming back to our example, the following Grammar-E2 is unambiguous and equivalent to Grammar-E1:

• E -> T | E "+" T | E "-" T | E "*" T
• T -> C | V | "(" E ")"
• C -> integer
• V -> identifier

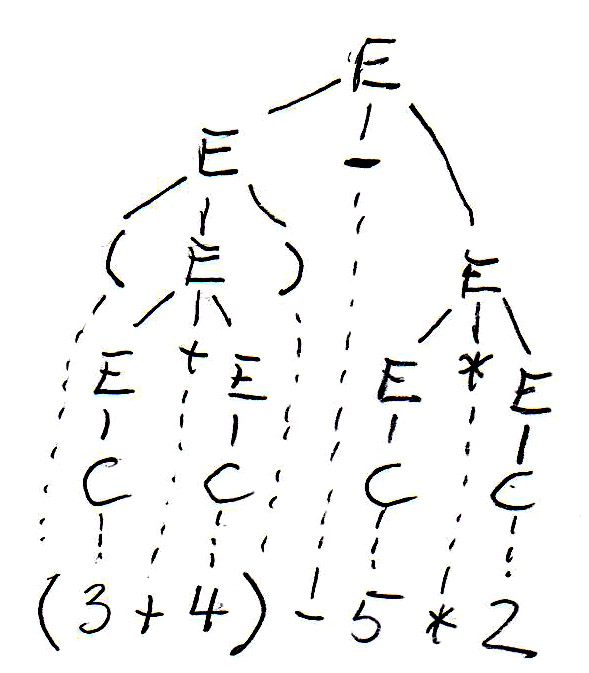
For the expression " (3 + 4) - 5 * 2 ", this grammar gives rise to the following syntax tree (on the left side):

Giving priorities to operators

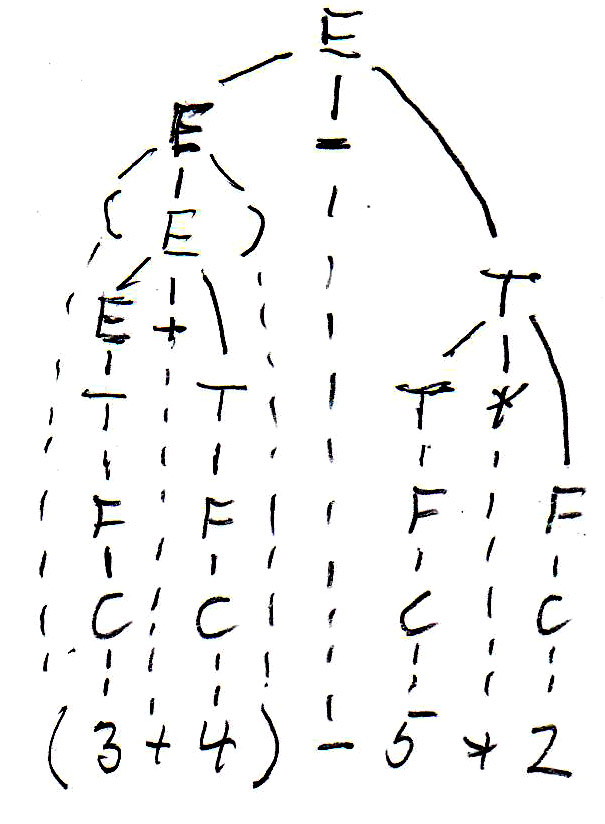As you can see, Grammar-E2 defines left-to-right evaluation for expressions, but does not give priority to multiplication over + and -. Since we always have bottom-up evaluation for expressions, we can introduce another nonterminal F, called "factor", which will always be below the nonterminal T, called "term", in the syntax tree (and therefore evaluated first), if we define Grammar-E3 as follows:

• E -> T | E "+" T | E "-" T
• T -> F | T "*" F
• F -> C | V | "(" E ")"
• C -> integer
• V -> identifier

Now we get the syntax tree for the expression " (3 + 4) - 5 * 2 " shown above (on the right side).

Abstract syntax - meta-models

Considering programs as strings of characters (or strings of lexical tokens) is fine for deciding whether a given string is a valid program, but it does not tell us what the meaning of the program is. In order to talk about the meaning of a program or of a spoken sentence, it is normally necessary to analyse the different parts of the program (or sentence) and find the meaning of the different components and their inter-relationships. One usually identifies different classes of components and identifies their relationships. Each class normally represents a concept (or construction) of the language. Therefore, one sometimes uses UML class diagrams to represent these issues. Such a class diagram is often called a meta-model or abstract syntax of the language.

These concepts are quite intuitive. Here is an example from the Java programming language to explain the issues. We consider only a small subset of the Java semantics, namely Java statements (assignment, if and while statements) that use variables and expressions. Here is a UML Class diagram showing the relationship between these concepts.

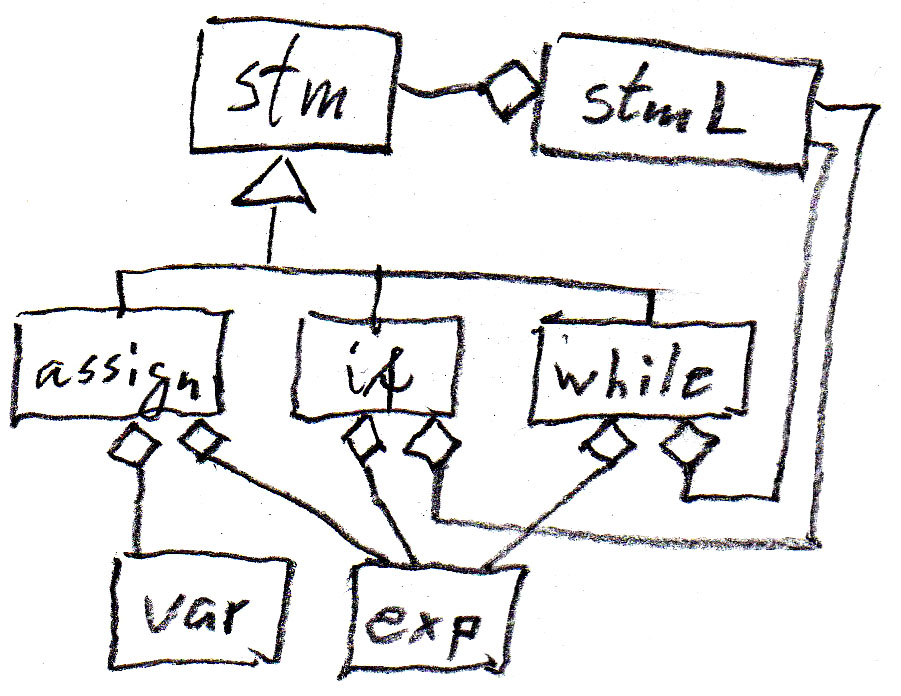
We can represent the "contains" relationships in the diagram by syntax rules as shown in the following table (assign is an assignment statement, if is an if-statement without else, while is a while-statement, stm is a statement, and stmL is a list of statements). Note that these abstract syntax rules are less abstract than the meta-model, since they introduce an order from left to write for the dependent components of an entity.

assign --> var exp if --> exp stmL while --> exp stmL stmL --> (stm)*

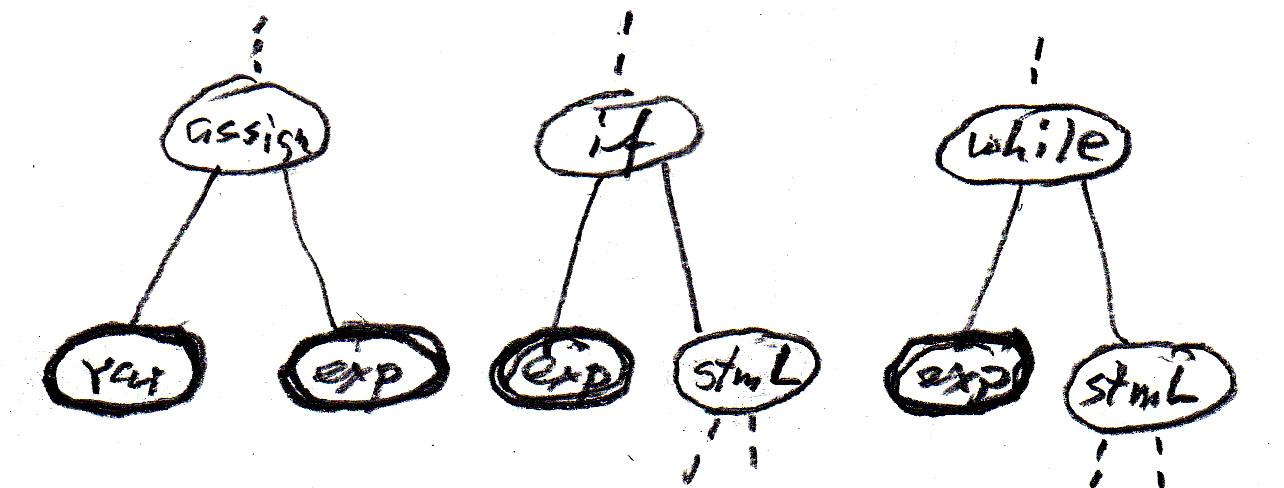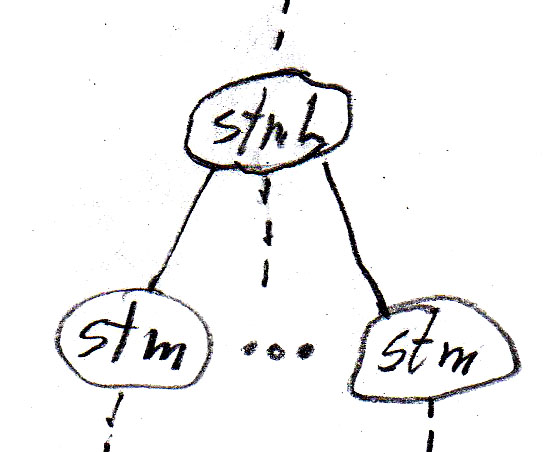The inheritance relations may also be represented by syntax rules (in the sense of "can be defined as") as follows:

• stm --> assign
• stm --> if
• stm --> while

Note that in this context (where we ignore the details of the variables and expressions) the concepts var and exp can be considered as terminal symbols; the other symbols are non-terminals.

Abstract syntax trees

Let us consider the Java statement

if (b) {while (a < 10.0) {a = a + addOn();} supplement = a - 10.0;}

Using the above abstract syntax rules and considering var and exp as terminals, then the above Java statement corrresponds to the following sequence of terminal symbols: " exp exp var exp var exp " . This string, by itself, is not very interesting.

However, if we interpret the above abstract syntax rules as rules for constructing a syntax tree, we get a much more interesting result. Each syntax rule defines a possible relationship within the syntax tree, as defined by the tree fragments shown in the table above. We get the following tree for the example Java program, which clearly shows the structure of the program example - which is important for the understanding of the meaning of this program.

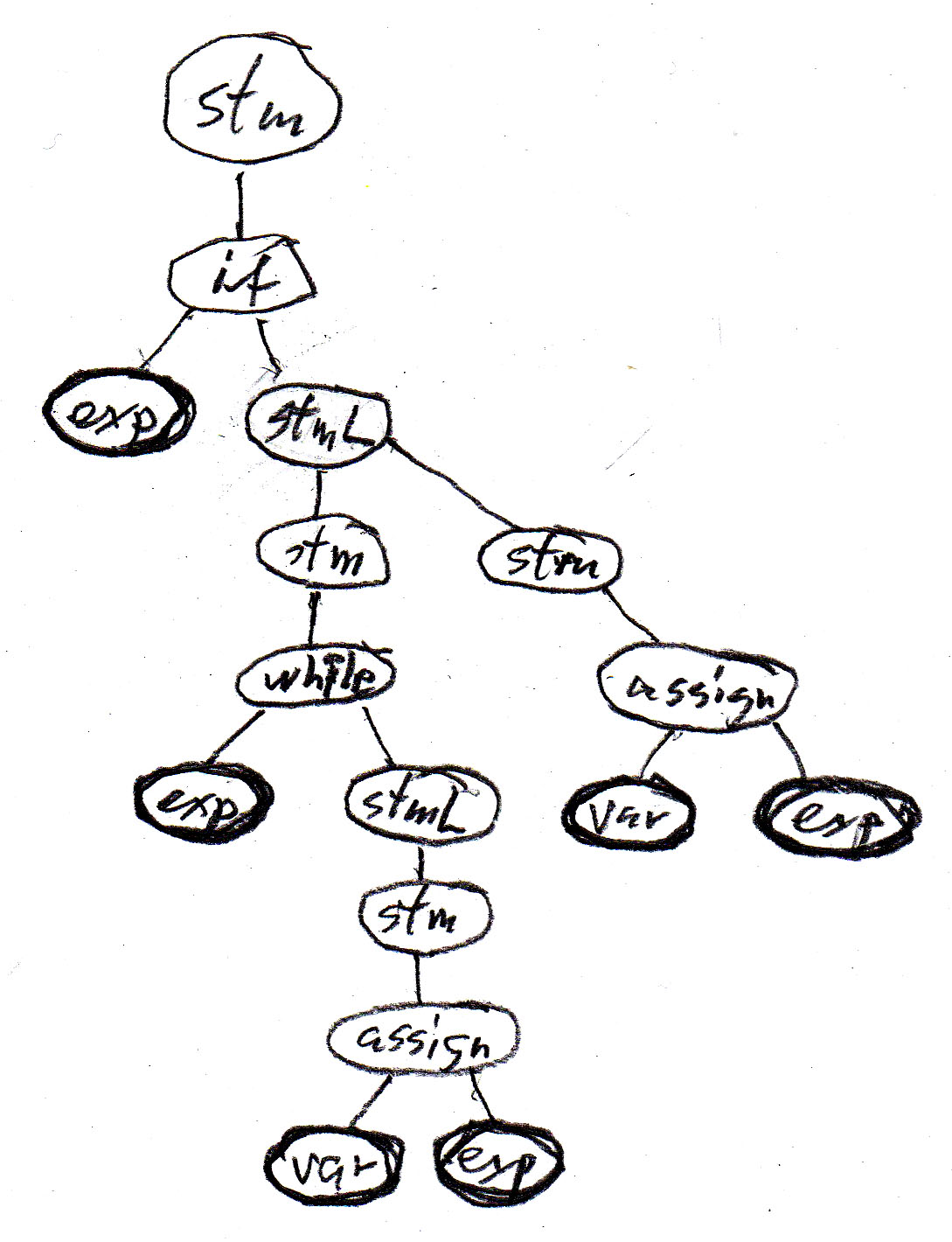
Note that all possible syntax trees can be constructed by interative substitution from the syntax (or syntax tree) rules.

More compact syntax rules

In order to reduce the number of synax rules, one often sees grammars where the inheritance relationships are not explicitly shown. For instance, the seven rules of our example above could be replace by the following four rules, which form an equivalent grammar. Note, however, that in this case the rules for if and while statements are identical (which means that the abstract syntax cannot distinguish them) - this difficulty disappears when "syntactic sugar" is added (see below).

• stm --> var exp -- assignment
• stm --> exp stmL -- if statement
• stm --> exp stmL -- while statement
• stmL --> (stm)*

The issue of obtaining a non-ambiguous (textual) concrete language syntax

The abstract syntax tree is good for understanding the meaning of a program, but not good enough to analyse a given program given in the form of a string of symbols. For instance, if we change (in the example program above) the if-statement to a while-statement, the sequence of resulting terminal symbols is also " exp exp var exp var exp " - this means we cannot distinguish these two programs by their sequence of abstract var and exp instances. Also a program of the form " if (b) {while (a < 10.0) {a = a + addOn(); supplement = a - 10.0;}} " would have the same sequence of abstract terminal symbols, although the structure of its abstract syntax tree is clearly quite different.

As we have seen above, the abstract syntax for the Java statements is ambiguous. In order to avoid such difficulties, one normally defines a so-called concrete syntax which complements the abstract syntax (the meaning) by introducing additional lexical elements that must be included in the program text, and which are selected in such a manner that any ambiguity is avoided.

For instance, the left concrete syntax below corresponds to what the designers of Java have decided about the syntax of statements. The syntax on the right corresponds to the Pascal programming language. Both have the same abstract syntax and meta-model - and the same meaning for their statements - only the "syntactic sugar" is different. The "syntactic sugar" is written in red.

With the Java concrete syntax given above, the abstract syntax tree of the example program becomes the syntax tree of the program shown below, which has a sequence of terminal symbols that correspond directly to the token sequence of the program text.

XML as a general concrete syntax

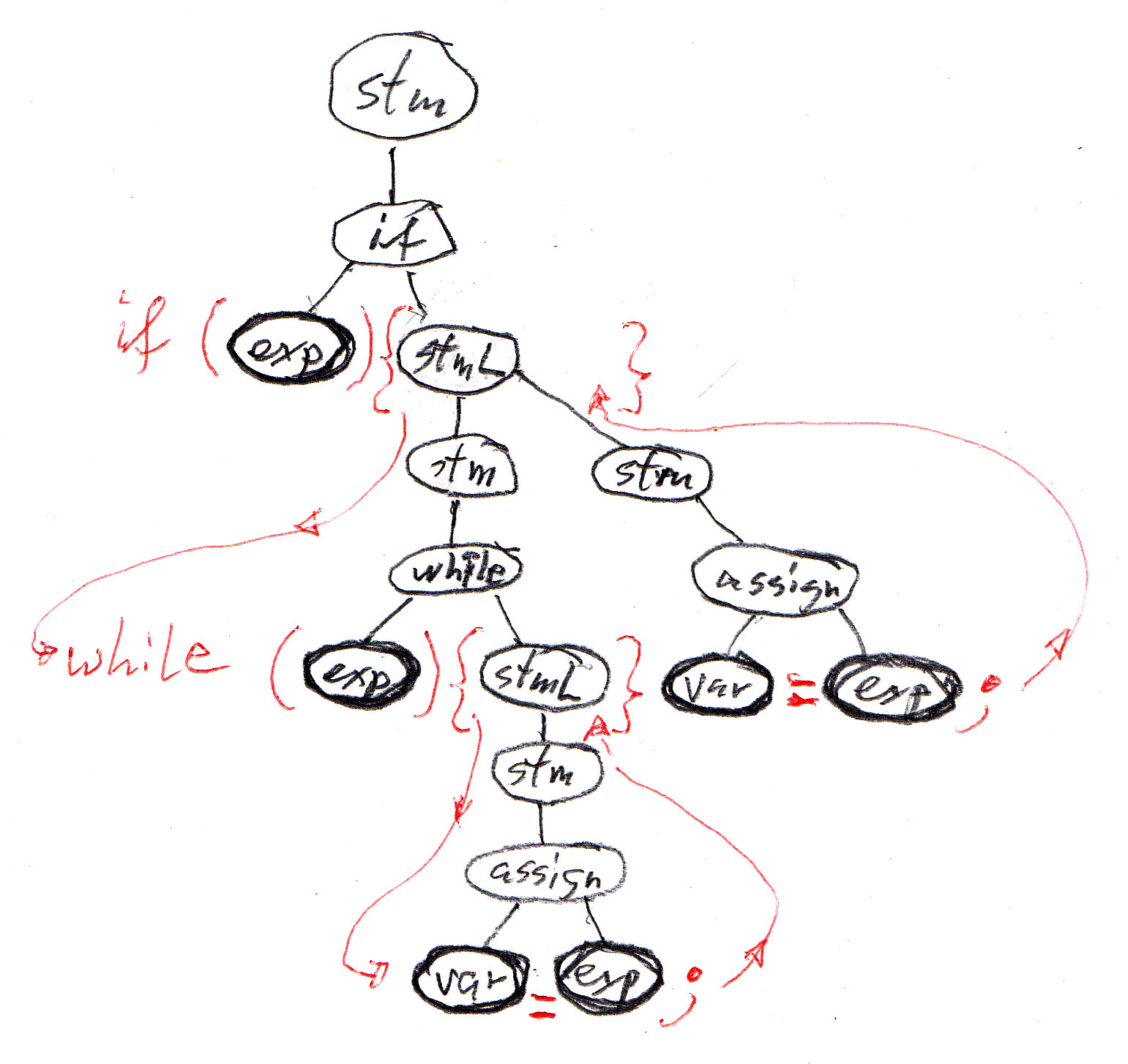
XML defines a character string representation of abstract trees, called DOM ("document object model"), which is often used for representing objects when they are transmitted over a network or stored as a character string in a database. In XML, each node of the abstract tree is called an "element", and elements may be of different types. The string representation of these elements and their subtrees follow a standard encoding convention that uses the names of the element types in the string encoding. Each element type may have attributes, and all elements have a kind of default attribute which is a character string.

The abstract syntax tree of the Java program above, when encoded as an XML string, may look as follows (note that the indentation has no meaning, it is only introduced to make the string more readable). In this case, all elements have no attributes, nor any default attribute string. The tokens <xxx> and </xxx> represent the beginning and the ending of an element of type "xxx" and its subtree. A token <xxx/> represents a "terminal" element without any subtree.

• <if>
  • <exp/>
  • <stmL>
    • <while>
      • <exp/>
      • <stmL>
        • <assign>
          • <var/>
          • <exp/>
        • </assign>
      • </stmL>
    • </while>
    • <assign>
      • <var/>
      • <exp/>
    • </assign>
  • </stmL>
• </if>

or (without indentation): <if> <exp/> <stmL> <while> <exp/> <stmL> <assign> <var/> <exp/> </assign> </stmL> </while> <assign> <var/> <exp/> </assign> </stmL </if>

For the interested reader (not formally part of this course)

• How to find a regular expression that defines the language accepted by an automaton ?
• Introduction to context-free grammars by example : defining the language of regular expressions

Syntax analysis: top-down and bottom-up

Here are two grammars that define the language defined by the regular expression c c* (a | b).

If one uses the grammar G2 to analyze the sentence "c c c a", one may construct the syntax tree by considering the following sequence of intermediate "sentential forms". At each step, one nonterminal in the current sentential form is replaced by the right side of one of the alternative syntax rules for this nonterminal. In the following, each line is a sentential form, and the nonterminal replaced in the next sentential form is shown in blue.

• S

• c C E
• c c C E
• c c C a
• c c c C a
• c c c a

Such a sequence is called a "derivation". One may also consider derivations more systematically, for instance, left-most derivations (where always the left-most nonterminal is expanded) or right-most derivations. The following is a right-most derivation for the same sentence using grammar G1:

• S

• A
• C a
• D C a
• D D C a
• D D D a
• D D c a
• D c c a
• c c c a

And here is a left-most derivation for the same sentence using grammar G2:

• S : there is only one rule for S; it leads to

• c C E : one applies a rule for the first non-terminal (from the left), namely C; if we choose the second rule, we get
• c c C E : once more the same
• c c c C E : one applies a rule for the first non-terminal (from the left), namely C; if we choose the first rule, we get
• c c c E : one applies a rule for the first non-terminal (from the left), namely E; if we choose the first rule, we get
• c c c a

In the last derivation, in order to decide which rule to apply for the next step, it was sufficient to look at the non-terminal one position to the right to the prefix of the sentence that was already included in the (partially constructed) tree (shown in green). One calls this "look-ahead" of one symbol. The analysis was done by constructing the tree from the top down; this is called top-down analysis. For any grammar in general, one can not always work with a bounded look-ahead. For example, if we use the grammar G1 for top-down analysis, we have to decide at the beginning which of the two rules for S should be applied; however, in order to make this decision, one has to look ahead up to the last symbol of the sentence (which could be a or b). Since the sentences have no bounded length, there is no bounded look-ahead of k symbols (for any given k) that is sufficient to make such a decision for all sentences. Top-down syntax analysis with a k-symbol look-ahead is called LL(k) analysis (first L for "from left to right" and second L for "left-most derivation").

Another popular analysis technique is LR(k) (which stands for "from left to right" and "right-most derivations"). Grammar G1 is suitable for this technique. The syntax tree is built from the bottom up; for instance, consider the right-most derivation with grammar G1 above, starting with the bottom line. At each step, only one next symbol from the input string needs to be considered to make the decision about what syntax rule to apply; see below, where the next symbol is written in red and the nonterminal (in the next higher line) whose production was applied is written in blue.

• S

• A
• C a
• D C a
• D D C a
• D D D a
• D D c a
• D c c a
• c c c a

LL(k) and LR(k) parsing methods are deterministic: at each step, a deterministic decision can be made about which syntax rule to apply to build the syntax tree. This implies that the grammar must be non-ambiguous, since an ambiguous grammars may allow for several syntax tree for a given input string. However, there are also non-ambiguous grammars that do not allow for LL(k) nor LR(k) parsing.

It is important to note that one can always (for any context-free grammar) do bottom-up or top-down analysis if one allows for a non-deterministic approach (similar to non-deterministic automata). However, such a procedure is in general not very efficient - because of the need for backing up in case of an unsuitable choice of production rule. Therefore one is interested in grammars that allow deterministic parsing. If a grammar allows for deterministic top-down [or bottom-up] analysis with k symbols of look-ahead, one says that the grammar is LL(k) [ or LR(k) ]. For allowing such parsing methods, the grammars must satisfy certain conditions (which will be discussed below for LL(1) grammars).

Note: In contrast to non-deterministic automata, in the case of context-free grammars that do not allow deterministic LL(k) nor LR(k) parsing, there is no algorithm to find an equivalent grammar that allows deterministic parsing. We saw that this is different for regular languages: for a non-deterministic accepting automaton, there is an algorithm for finding an equivalent deterministic one.

Top-down analysis for LL(1) grammars ["recursive descent parsing"]

Principle of LL(1) parsing

Here is another example of a grammar: Grammar G3:

• S --> A   B   C 
• A --> D   B  |  C
• B --> b  A   d  |  c
• C --> ε  |  e  C
• D --> a  |  f  A

Here is a left-most derivation of the sentence "a b e d c $" (where $ repesents the end of the string - end of file). In each line, the left-most nonterminal, which is replaced in the next line by the right side of one of the syntax rules, is written in red. The replacement is written in italic. On the right is the corresponding syntax tree (terminal symbols underlined).

In order to perform a deterministic top-down syntax analysis with a single symbol of look-ahead, we have to decide for each line of the derivation, which syntax rule is to be applied for the left-most nonterminal (written in red), based solely on the information provided by the next input symbol, which is a symbol of the given sentence (line 10) which is written in the position below the nonterminal in question (the next terminal symbol which is not yet part of the syntax tree at this point of the derivation). This means the choice of the alternative (if there is more than one alternative) depends only on the left-most nonterminal and the next input symbol.

It is therefore natural to construct a so-called parsing (or syntax) table that indicates for each nonterminal of the grammar and each input symbol which syntax rule (i.e. which right side) should be applied. Note that for certain nonterminals, certain input symbols should not be the next one - if they are, this represents a syntax error of the input string. Here is the parsing table for the grammar G3 (en empty table entry represents a syntax error). Note: A bnlack entry in the table is the right side for which the symbol of the column is in the First; a blue entry indicates that the symbol of the column is in the Follow of the nonterminal of the table row (and the entry is the right side which could generate the empty string).

Implementation of LL(1) parsing (a) : the interpretive approach

A simple approach to the implementation of LL(1) parsing is to build an interpreter program that uses the information in the parsing table and produces the left-most derivation discussed above. One need a "reading head" that reads the given input string from left to right and always indicates the next symbol to be considered. The other information that the interpreter must remember is the intermediate sentenial form (i.e. the content of the current line in the derivation discussed above). This sentenial form consists of two parts: on the left is the part of the input string that is already included in the partically constructed syntax tree, and on the right is a string of nonterminals and terminals which starts with the left-most nonterminal to be replaced. It is convenient to store this right part in a stack data structure with the left-most nonterminal on the top of the stack. This is the approach used in the interpretive algorithm described in the book by Aho et al. (see below).

This is the interpreter program:

Here is an example of a grammar and the corresponding syntax table:

 . . . and the execution trace of the interpreter for the sentence "id + id * id"

Implementation of LL(1) parsing (b) : using recursive procedures (to be used in Lab 8 and Assignment 3)

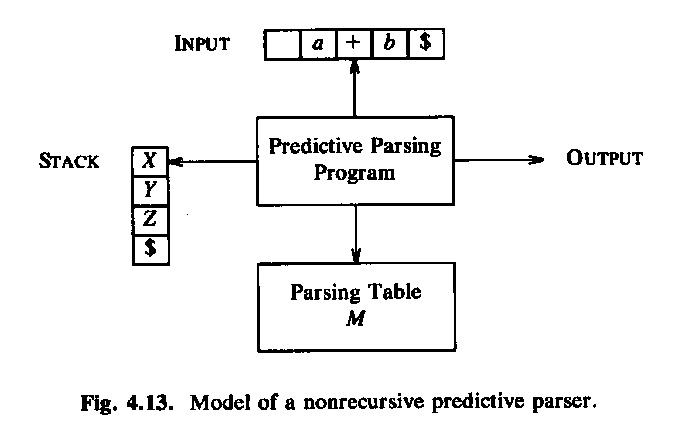
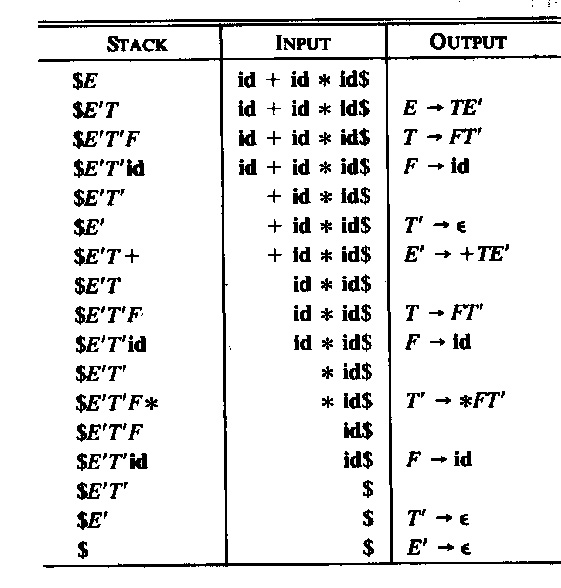
Another approach to the implementation of LL(1) parsing is to use recursive procedures, one for each non-terminal of the language. These procedures call one another recursively. Each procedure realizes the rules that are defined for the non-terminal in question. For example, for grammar G3, one could write the following Java procedure (note that the variable char symb contains always the next symbol (the look-ahead) and the procedure next() is used to read the next symbol). The main calls the procedure S() and verifies, when S returns, that the next symbol is end-of-file. Note that the abbreviation "symb in {'a', 'b', 'c', 'e', 'f'}" does not follow the Java syntax and must be rewritten in order to obtain a valid Java program.

Verification of the LL(1) property

Here is the grammar G3 again:

• S --> A   B   C   
• A --> D   B  |  C
• B --> b  A   d  |  c
• C --> ε  |  e  C
• D --> a  |  f  A

Please note that each of the following modifications of the grammar G3 will make it non-LL(1):

1. The second rule for D becomes D --> e A : The choice between the two alternatives of A will not be possible if the next symbol is an e.
2. The second rule for C becomes C --> d C : The choice between the two alternatives of C will not be possible if the next symbol is d, because C may be called by the second rule of A, and A can be followed by d (see first rule of B). Therefore the next symbol d may correspond to the d in the first rule of B (then the rule C --> ε should be applied), or it may correspond to the second rule of C.

To avoid problems like under point (1) above, one has to verify for each nonterminal that has several alternatives, that there is no symbol that could be the first symbol of a string generated by one alternatives and also be generated as the first symbol of another string by another alternative. One calls the set of terminal symbols that may appear as the first symbol of a string generated by a nonterminal X, the set First(X). Similarly, one calls First(right side) the set of terminals that could appear as the first symbol of a string generated by the given right side of a syntax rule. To avoid the problems such as under point (1) above, we therefore have the following constraint on the grammar: If a nonterminal has several alternatives, then the First sets of all alternatives must be disjoint (that is, they should not contain any common symbol).

To avoid problems like under point (2) above, we have to check some additional rule if one of the nonterminals may generate the empty string - because in this case the next symbol of the look-ahead may not correspond to the First of this nonterminal, but rather to one of the symbols that may follow the substring generated by the nonterminal within the overall input string. The set of terminals that may follow a string generated by a nonterminal X within the context of a valid sentence of the grammar is called Follow(X). To avoid the problems such as under point (2) above, we therefore have the following constraint on the grammar: If a nonterminal X can generate the emtpy word, then Follow(X) must be disjoint from the First of all alternatives. But this is equivalent to requiring that: If a nonterminal X can generate the emtpy word, then Follow(X) must be disjoint from the First(X). In order to determine whether a nonterminal can generate the empty string, one normally includes the symbol  "ε" in the set First(X) if X can generate the empty string (although this symbol is not formally an input symbol).

LL(1) condition: In summary, one can say that a grammar has the LL(1) property if the following two conditions are satisfied by all non-terminals of the grammar:

• For all non-terminals, the First sets for all alternative right sides are disjoint.

• For all non-terminals: If the First set of one alternative contains "ε" then the Follow of the non-terminal must be disjoint with the First set of the non-terminal.

Calculating First and Follow sets

Note: The rules to calculate the sets First and Follow are formulated in a form which corresponds to the iterative substitution which we discussed at the beginning of this chapter.

The following calculation rules must be applied interatively until there are no further additions to the sets First and Follow. Initially, one may assume that these sets are all empty. The sets First can be calculated first, since they do not depend on the Follow sets. Here is an alternate presentation of this topic.

First

• For a terminal X, the First set is : First(X) = {X}
• For a nonterminal X, the First set is : First(X) = union of the first First sets of all right sides of the alternative production rules.
• For the right side of a production rule of the form "ε":  First(ε) = {ε}
• For the right side of a production rule of the form X₁ X₂ ... X_n:
  • First*(X1) is included in First(X₁ X₂ ... X_n) where First*(Y) = First(Y) minus "ε" (if it is included in First(Y))
  • If the sets First(X_i ) include "ε" for all i = 1 ... k, then First*( X_k+1 ) is included in First(X₁ X₂ ... X_n)
  • If all sets First(X_i ) include "ε" then First(X₁ X₂ ... X_n) includes "ε"

Follow

• In order to define more clearly where the end of the program is, one may introduce a marker, for instance $, which has to follow at the end of a valid program. The marker is not really a symbol of the language; in order to simplify the detection of the end of a program, one defines Follow(S) ={$}.
• If there is a right side of some production rule of the form "alpha X beta", where alpha and beta are sequences of symbols (alpha may be empty, while beta should be non-emtpy) and X is a non-terminal, then First(beta) is added to Follow(X), except ε if ε is contained in First(beta).
• If there is a rule of the form "A -> alpha X beta" where beta is empty or First(beta) contains ε, then Follow(A) is added to Follow(X).

Example: Calculating the First and Follow sets for the grammar G3

Calculating the Follow sets for the nonterminals that can generate the empty string:

• We need to calculate Follow(C) and Follow(A).
• Calculating Follow(A): A is at the end of a right side of D, therefore Follow(A) includes Follow(D). In rule 3, A is followed by d, therefore d is included in Follow(A). In rule 1, A is followed by B, therefore First(B) is included in Follow(A). Therefore Follow(A) = Follow(D) union {d} union First(B).
  • Follow(D) = First(B) since D occurs only once on the right side of rule 2 before B.
  • Therefore Follow(A) = {d} union First(B) = {b, c, d}
• Calculating Follow(C): C occurs at the end of the second right side of rule 2 - this does not give any contribution to Follow(C) because the left symbol is also C. C is also at the end of the second right side of rule 2 - therefore Follow(C) includes Follow(A). C is also at the end of rule 1 - therefore Follow(C) includes {$}. In summary, Follow(C) = {b, c, d, $}

Checking the LL(1) property and building the parsing table

Once the sets First and Follow have been calculated, one can check that the grammar is LL(1) by verifying the two properties discussed above. These properties ensure that the parsing table admits at most one alternative in each entry of the table.

In fact, the sets First and Follow are very useful to define the parsing table. We can follow the following procedure to fill in the entries in the parsing table. For an entry for nonterminal X and next terminal symbol y, the entry is found as follows:

• If there is an alternative rule for X such that y is in First(alternative) then enter this alternative in the table entry.
• If there is an alternative rule for X that generates the empty string (that is, "ε" is in First(alternative) ) and y is in Follow(X) then enter this alternative in the table entry.
• Otherwise, the entry of the parsing table remains empty.

Transforming a grammar to make it LL(1)

(1) Combine common prefixes: If several production rules for the same non-terminal contain some common prefix (for instance A --> a B c  |  a B A ), one can incorporate this prefix in a new rule (the example becomes A --> a B A'  and   A' --> c | A ).

(2) Elimination of left recursion: A grammar with left recursion (for instance A --> A c b | a ) leads to infinite loops during the analysis (by recursive procedures, or by using a parsing table). Such a grammar is not LL(1), by the way.

Definition: A grammar has left recursion if it contains a non-terminal, say A, from which it is possible to derive a string " A Y " where Y is any string of terminal and/or non-terminal symbols.

When discussing the alternative definition of Kleene's operator at the beginning of this chapter, we saw that "immediate" left recursion (that is, without any intermediary non-termianl symbol) can be replace by right recursion. This general rule discussed with Example 4 leads to the following elimination recipee:

• A --> Aa | b     can be replaced by
  • A -->  b A’
  • A’ --> a A’ |  ε
• A --> A a1 | A a2 | … | A am | b1 | b2 |…| bn        can be replaced by
  • A --> b1 A’ | b2 A’ | …| bnA’
  • A’ --> a1 A’ | a2 A’ |… am A’ | ε

For more complex cases, one can use the following algorithm (taken from the book by Aho):

Here are some examples

Syntax diagrams – and extended BNF

Here is an example grammar for numerical expressions:

1. E → T E'
2. E' → "+" T E'   |  ε
3. T → F T'
4. T' → "*" F T'   |  ε
5. F → "(" E ")"   |  id

Sometimes one uses extended BNF notation for defining the syntax, where parenthesis, Kleene's star and the ?(optional) operator are allowed. Then the right side of a syntax rule could in general define a regular expression involving terminal symbols, but also nonterminals. For instance, we know that the recursive equation " T' = "*" F T'   |  ε " has the solution T' = ( "*" F )* - notice that "*" is a terminal symbol and the * after the closing parenthesis is Kleene's star operator. Therefore the rules (3) and (4) above could be equivalently rewritten as

6. T = F ( "*" F )*

Syntax diagrams

Syntactic rules can also be defined in graphical notation similar to state machines. Such syntax descriptions are called "syntax diagrams". Below (left) are such diagrams for the syntax rules (1), (2) and (5). In the middle is a syntax diagram corresponding to rule (6) above. It is important to realize that each syntax graph is a recursive state machine, this means, it behaves like a state machine, except that certain transitions do not correspond to the reading of an input symbol, but instead represent the (recursive) call of another state machine instance. A recursive state machine equivalent to the syntax diagram for T (in the middle) is shown on the right - the double arrow transitions represent the calling of an instance of the F-stateMachine.

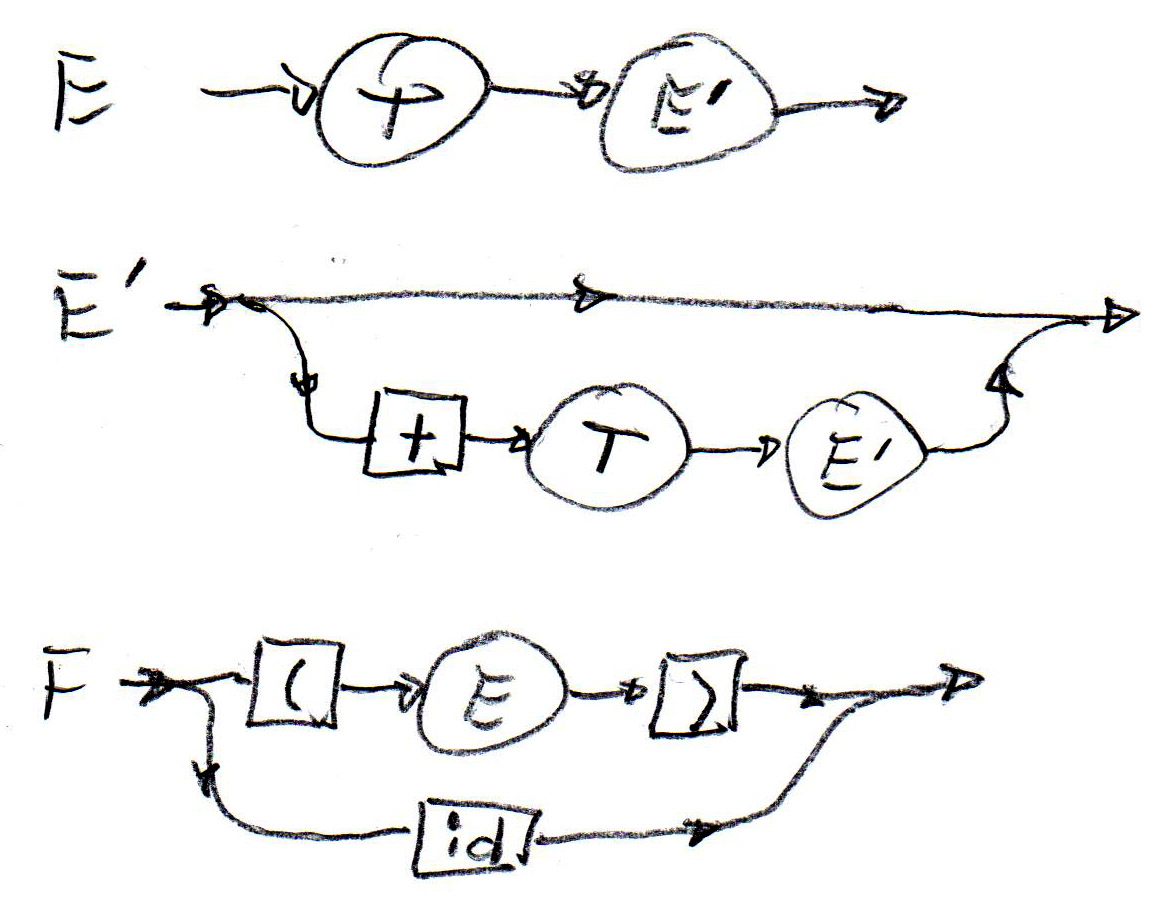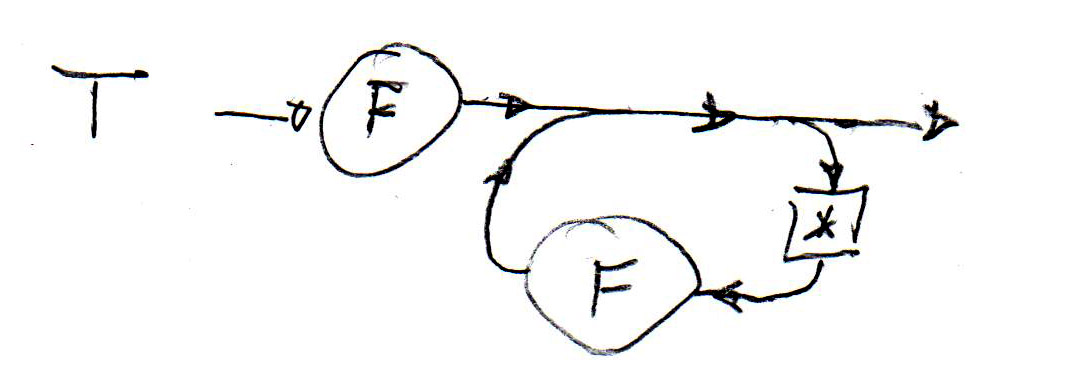Recursive automaton for T:

Note that these syntax diagrams (or the corresponding recursive state machines) can be easily implemented by recursive procedures, as proposed for the implementation of LL(1) parsing with recursive procedures. For instance, syntax structures as shown for T above can be easily realized by a method with a loop, such as the following:

• void T() { F(); while (symb == '*') { next(); F(); } }

When one builds a syntax analyser using recursive procedures, one often tries to reduce the number of procedures as compared with the number of nonterminals in the original syntax. Replacing the rules (3) and (4) by rule (6) and then using the diagram above is an example for such a reduction.

Handling syntax errors (see here or here) – this is not part of the course content (provided for the curious reader)

Semantic attributes

For the description of semantic properties of the syntactic constructs of a language, one often uses so-called semantic attributes - attributes of the syntactic non-terminals (and sometimes terminals). As an example, one may think about the classes of non-terminals defined above in the section on abstract syntax. An expression object may have an attribute defining the data type of the expression, a variable object may have an attribute defining the type of the variable, and a statement and expression object may have an attribute that contains the generated code for representing this object in the generated object code.

See Section 3.5 in the book by Sebesta for an explanation of

• the use of semantic attributes, in general,

• the rules for the evaluation of the values of the semantic attributes over a given syntax tree, and
• the definition of semantic constraints (that depend on semantic attributes) that represent certain semantic conditions that must be satisfied by a valid program; since these conditions can be verified by the compiler, they are called static constraints; in opposition, certain constraints that can only be verified during the program execution are called dynamic constraints. Examples ?

Here are the diagrams showing an example in the book: definition of the attribute grammar, definition + tree example

Note: The attribute evaluation rules, in their restricted form to avoid circular definitions (as mentioned in Section 3.5.3 in the book by Sebesta), were first proposed in my publication "Semantic evaluation from left to right" which appeared in the (then) prestigious journal of the ACM in 1976. Here is an example from that article which shows the rules defining the scoping rules of a programming language; in fact, it shows how the information included in the partial symbol tables is passed between the different parts of the program.

Example: different grammars for expressions and static evaluation of the values of expressions

Static evaluation means evaluation during the compilation phase (as opposed to during the execution phase). The evaluation of semantic attributes is performed during the compilation phase. What kind of attributes are required for the evaluation of the value of expressions ? - This depends on the grammar rules. In the following, we want to evaluate the semantic attributes during a single depth-first pass through the syntax tree - that is, in parallel with the syntax analysis using the recursive decent LL(1) parsing approach.

We have seen the following three forms of sytax definition for simple expressions:

1. E(0) --> T | E(1) + T | E(1) - T

2. E --> T(1) ( (+ | -) T(2) )*
3. E --> T E' and E'(0) -->  ε | + T E'(1) | - T E'(1)

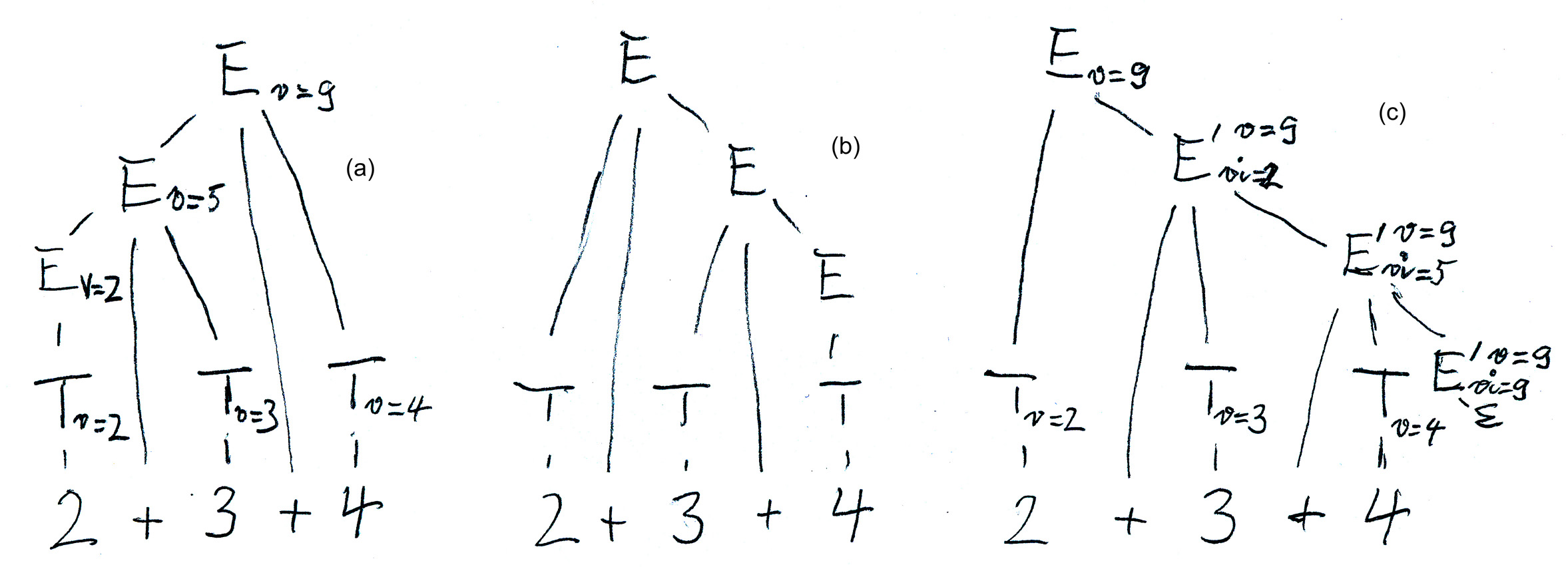
With the grammar (1) we need one synthesized attribute "v" (for value) for the nonterminal E which is evaluated on the syntax tree from the bottom up and from the left to right, as seen in Figure (a) below. - However, grammar (1) is not suitable for LL(1) syntax analysis. - Here are the evaluation rules for the attributes:

• for the first alternative: v(E(0) ) := v(T)

• for the second alternative: v(E(0) ) := v(E(1) ) + v(T)
• for the third alternative: similar

With grammar (3), which is obtained from grammar (1) by applying the transformation rule discussed earlier, we get a syntax tree as shown in Figure (b) below. With bottom-up attribute evaluation, we get an evaluation from the right to the left, which is not what we need. However, we can introduce two attributes for E', a synthesized attribute called "v" (as for the nonterminal E above), plus an inherited attributed called "vi" which represents the intermediate value of the expression evaluated up to the non-terminal node E' in question. Here are the evaluation rules for the attributes (see also Figure (c) below):

• for the rule E --> T E' : vi(E') := v(T) --- v(E) := v(E')

• for the rule E'(0) -->  ε : v(E(0) ) := vi(E(0) )
• for the rule E'(0) --> + T E'(1) : vi(E(1) ) := vi(E(0) ) + v(T) --- v(E(0) ) := v(E(1) )

Here is a sketch of a recursive procedure realizing the syntax analysis and semantic evaluation for E'. Note that the synthesized attribute is simply programmed as a value returned by the parsing procedure, and the inherited attribute is simply represented by a parameter of the procedure.

• int parse_Eprime (int vi) { if(token != PLUS) {return (vi)}else {next_token(); int T_v = parse_T(); return( parse_Eprime (vi + T_v)); } }

With grammar (2): We note that the attribute evaluation rules for grammar (3) are complicated. The situation becomes much simpler if one uses the grammar (2). It also has the advantage over grammar (3) that it has only one nonterminal, and therefore a single recursive procedure is enough (instead of two, one for E and one for E' in the case of grammar (3)). The following is a sketch of such a recursive procedure written in Java according to the syntactic diagram below.

• int parse_E () { int v = parse_T(); while (token == PLUS) {next_token(); int T_v = parse_T(); v = v + T_v; } return(v); }

Notes on the semantics of programming languages (see here) – this is not part of the course content (provided for the curious reader)

The four classes of grammars à la Chomski

Chomsky distinguished the following four classes of grammars (from the most general to the most restrictive form):

• General grammar: The grammar is a set of production rules, where the left side and the right side of each rule are strings of non-terminal and terminal symbols. A rule "left side" --> "right side" means that the string "left side" can be replaced within a derivation by the string "right side".

• Grammars with context: As above, but the length of the right side of a rule may not be shorter than the length of the left side. Note: Often the left side consists of a non-terminal symbol " in its context", which means a non-terminal is preceeded or succeeded by strings of other terminal or non-terminals which represent the context and that appear in the same form in the right side of the rule; however, the non-terminal in question is replaced, in the right side, by some string. The rule is like a rule of a context-free grammar where the same context is added on the left and right sides of the rule.
• Context-free grammas: As above, except that the left side must be a single non-terminal. Note 1: This corresponds to the BNF notation. Note 2: This rules out to have the empty string on the right side of a rule. However, it has been shown that for a grammar that has such a rule, one can find an equivalent context-free grammar that does not have the empty string as a right side of a rule.
• Regular grammar: As above, except that the right side of a rule contains at most one terminal and one non-terminal. Note: For each regular grammar, one can find a finite state automaton that accepts the language defined by the grammar, and inversely. Therefore the language may be defined by a regular expression. Thus the name "regular grammar".

A (formal) language is a subset of all the symbol sequences that can be formed from the alphabet of the terminal symbols. In general, there is no bound on the length of these sequences (the sentences of the language), most languages are infinite (that is, have an infinite set of sentences). Therefore the following questions arise:

• How can we define such an infinite language using a finite description ? - One needs a finite description to reason about it.

  • Chomski's grammars give a possible answer: Each grammar only contains a finite set of rules.
• Enumeration problem: How can we enumerate all sentences of a language ? - That is, is there a procedure (that would not terminate for infinite languages) that will produce all sentences, one after the other ?
  • This can be done based on the given grammar of the language: the procedure goes through all possible applications of grammar rules considering all possibilities (breadth-first approach must be used, because with a depth-first approach one may not get all possibilities (just going down one possible branch of the infinite tree).
• Recognition problem: How can we determine whether a given sequence of terminals belongs to the language ?
  • How this can be done depends largely on the form of the grammar:
    • For general grammars, this problem is undecidable.
    • For grammars with context, this can be solved by enumerating all sentences in increasing order of their length. If all sentences with the same length as the given sentence have been enumerated, one can make the decision. Quite inefficient algorithm, in general.
    • For context-free grammars different approaches exist, but each approach is normally limited to subsets of context-free grammars that satisfy certain additional restrictions, such as the LL(1) property.
    • For regular grammars, one usually finds the corresponding deterministic automaton which represents an efficient recognition algorithm
  • Another approach to solving the recognition problem is to find for each given grammar an automaton that can recognize whether a given sentence belongs to the language. For regular languages, one can find always a finite state automaton that accepts the language in question. For the more general types of grammars, one needs to find more powerful types of automata that could do the job. For context-free grammars, these are non-deterministic push-down automata (similar to the interpretive LL(1) parsing algorithm that uses a syntax table). For general grammars, one has to use Turing machines. Unfortunately, they may not halt (loop forever), therefore not providing a solution. Some diagrams showing these machines are given here.

Undecidable problems

A problem is undecidable if it can be shown that there exist no algorithm that makes a decision for all possible cases. - In a sense, one may say that the problem is "more complex" than problems that are NP complete, because for those problems there are algorithms, although not very efficient.

Examples of undecidable problems:

• Halting problem of Turing Machines (this is a very famous example, because in this context, the existance of undecidable problems was detected by Turing) - here is a simple proof

• Recognition problem for general grammars (see above)
• The question whether two context-free grammars are equivalent
• The question whether a given context-free grammar is ambiguous
• The question whether a given context-free grammar with semantic attribute evaluation rules may give rise to circular definitions on some of the possible syntax trees

Note: All questions related to regular languages are decidable.

Translated from French and revised: Februar 2008; updated 2009, 2010, 2011, 2012, 2013, March 16, 2015