Lexical analysis (formal languages, regular expressions and accepting automata)

Course notes for Section 2, Chapter 2.2 of the course SEG 2106
by Gregor v. Bochmann, February 2004 (translated to English: January 2008, revised 2009, 2010, 2012, 2013, 2015)

Formal languages

When talking about formal languages, one tries to define simple and precise rules for determining which sequence of symbols (characters, or lexemes, or other things) is valid. Using a mathematical approach, one can establish definition formalisms for languages that are closely related to algorithms for the generation and recognition problems. The approach can be applied separately to lexical analysis and syntax analysis for real languages.

The definition of a formal language starts with the definition of an alphabet A which is a set of symbols. Then one considers the set of all finite-length sequences of symbols, (also called chains, or words) which is denoted by A*. This set also includes the so-called empty word (the sequence of length zero; written epsilon (є) or lambda).

Definition: A language is a subset of A*. - - The elements of a language are called the valid sequences or the sentences (or words) of the language. Here are some examples of languages (L1 through L4):

• A = {a, b, c}; L1 = {є, a, ab, ccc}; L2 = {x є A* such that the length of x is even}
• A = { (, ), a}; L3 = {x є A* such that the paranthesis in x are "well structured"}
• A = {a, b, c}; L4 = {x є A* such that xt can be obtained by concatenation (any number of times) from the following three sequences: ab, accc, bcbc, c, aca, bbb }

Operations on chains

Given an alphabet A, one can define the following operations on the sequences in A*:

• Concaténation (example:  ac . bc = acbc)

• Exponentiation (multiple concatenation with itself) (examples: (ab)³ = ab. ab. ab ; a⁰ = є )

Operations on languages

On the set of all languages over A (that is, languages formed from alphabet A, that is, subsets of A*) one can use the following operators (see also definitions in book by Aho):

• the general operators defined on sets (since a language is a set of sequences), such as

  • union (example: L1 U L2 = set of sequences that are either in L1 or in L2 or in both)
  • intersection (example: L1 ∩ L2 = set of sequences that are in L1 and in L2 )
• the operators defined on sequences (as described above), but now applied to set of sequences:
  • Concaténation (example: L1 . L2 = { x . y where x є L1 and y є L2}
  • Finite exponentiation (example: L1ⁿ  = L1 . L1 .  ... L1  (n times)  ; L⁰ contains only the empty word)
• Kleene's operator: Given a language L, one can define a language consisting of all multiple concatenations of L, written L*. More precisely, L* = union of Lⁿ over all n ≥0, or L^*  = U_{n ≥0}  Lⁿ . Note that this includes the emtpy word (n = 0).
  • In particular, if L consists of a single chain x, then x* is the set of all multiple concatenations of x with itself, including the empty word.
  • One also uses the notation L+ to denote all multiple concatenations of L excluding L⁰ .

Grammars

A grammar is a set of language equations, using the language operations above. Each equation is of the form "Y = Expression" where Y is a language variable, and Expression is a language expression containing (constant) chains and language variables that are related through the language operations defined above. The (constant) chains are sometimes called "terminal sequences" and are fixed sequences of alphabet symbols. Here are two example grammars:

• The language L2 defined in grammar G1 consists of all sequences consisting of a finite number of concatenated chains "ac". And L1 consists of the chain "abc" and all chains of L2 followed by the symbol "b".

Definition: A solution of a grammar is a set of languages, one for each language variable, such that all equations of the grammar are satisfied. - - The language defined by a grammar is the language associated with the first language variable in a solution of the grammar. - This variable is also called the root or starting symbol of the grammar.

Definition: Two grammars are equivalent if they define the same language. (Revision: An equivalence is a kind of relation. - What are the properties that an equivalence must satisfy ?)

Notes:

• Normally, the intersection operation and finite exponentiations are not used in grammar definitions.
• One distinguishes different kinds of grammars, as follows:
  • A grammar without recursive definitions of variables are called a regular grammar. And the language definied by such a grammar is called a regular language (see below).
  • A grammar (possibly with recursive definitions) using only the operators concatenation and union is called a context-free grammar (see next chapter in this course).
    • If it also uses Kleene's star operation, it is called an extended context-free grammar.
• A language definition in the form of a grammar is a useful tool for the generation of the valid sentences of the language. But it is in general not so useful for deciding whether a given chain is part of the language. For this purpose, one normally uses some kind of automata: in the case of regular languages, finite state accepting automata (LTS with certain accepting states) are used for this purpose. For the more general context-free languages, other deterministic algorithms can often be used (see chapter on syntax analysis).

Notations for defining grammars

The notation introduced above for defining a grammar in the form of a set of language equations is probably the most mathematical notation. There are other notations (that have the same meaning) which are often used. The most important are:

• Backus-Naur-Form (BNF): This notation was developed for defining the grammar of Algol (in the 1950ies). It does not support Kleene's operator. It uses "-->" instead of "=" and instead of using the union operator, it has a "production rule" for each alternative in a union. Each production rule is terminated by a dot "." and constant strings are written without the {}. Contatenation is written without the dot. - - Grammar G2 would be defined as follows:
  • L1 --> x y z .
  • L1 --> L2 y .
  • L2 --> x z L1 x .
• There are different conventions for distinguishing between language variables and constant chains. In this course, I often use upper case characters to introduce laugage variables and I use lower-case characters for alphabet symbols. Sometimes, language variables are written within <> brackets, such as <L5>. As a general rule, identifiers that occur on the left side of an equation are language variables, also called non-terminal symbols, other things represent constant chains, also called terminal symbols or terminal chains.
• Extended BNF:
  • Often the union is simply written as "׀" (or sometimes "+")
  • Sometimes, the BNF notation allows for parenthesis on the right side of equations and for the use of Kleene's operator. Then grammar G1 could be written as follows:
    • L1 --> abc ׀ L2 b .
    • L2 --> ( ac )* .
• Regular definitions: They are written as above (extended BNF), however, using "=" instead of "-->". And there should be no recursion in the definitions. See example.
• Regular expressions (RE): This is a regular definition with a single equation. There are a number of extended notations that are often used with regular expressions, such as the following:
  • the "+" operator, as explained above.
  • the "?" operator meaning zero or one occurrence of the preceeding item.
  • classes of characters (example [A-Z]). See also extract from book.
  • ******

Regular languages

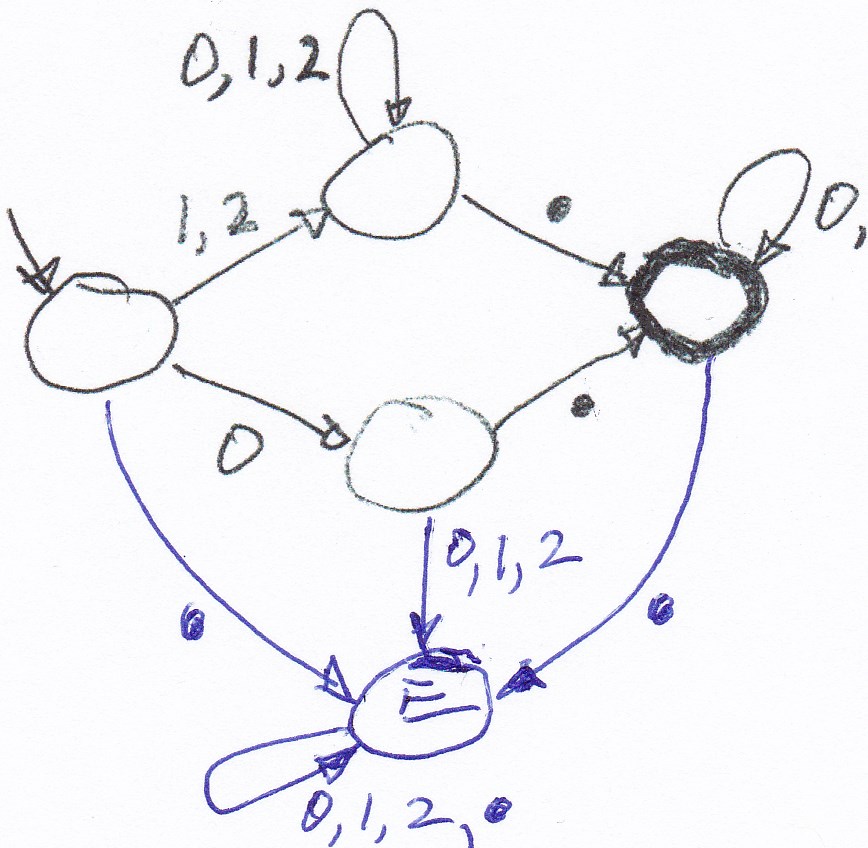
Example of real numbers: We consider the real numbers (based on a ternary system, using only the characters 0, 1, 2 and the point) which can be seen as a language over the alphabet{0, 1, 2, . }. We assume that a (single) zero is required before the ternary point if the number is smaller than 1. Examples of sequences that are not valid real numbers are 123 and 01.2  .  The following regular expression defines this set of real numbers: (0 | (1 | 2) (0 | 1 | 2)* ) . (0 | 1 | 2)* . Here are other simple examples.

Algebraic equivalence properties for regular expressions: The following equivalence properties can be used to determine whether two given regular expressions are equivalent (by substituting one side of one of these equations in a given regular expression by the other side of the equation, thus obtaining an expression that is equivalent to the given one). For instance, one can use equation (15) to show that ((a | b ) c )* (a | b ) is equivalent to (a | b ) (c (a | b ))* .

Finite State Automata (FSA) - or "acceptors") - similar to LTS

A Finite State Automaton (FSA) is a state machine with a finite number of states. One of the states is the initial state of the automaton, and a subset of the states are called accepting states. The input to the automaton is providing by a reading head which reads the symbols of an input string from left to right. Each symbol read is an input to the automaton. If there is no transition in the current state for the input symbol read, then the input string is not valid. When the reading head arrives at the end of the input sequence, the sequence is accepted if and only if the automaton is in an accepting state. Such an automaton is also called an acceptor automaton. We assume here that the automaton is deterministic, that is, for a given sequence of input symbols, the automaton can only be in one state. Note: This is nothing else than an LTS for which one has defined a subset of the states to be accepting.

Examples

Real numbers: An acceptor automaton for the language of real number (in the ternary system, as discussed above) is given by the following diagram (accepting states are drawn with think circles).

• Note: If the reading of the input sequence leads to a non-specified reception (a symbol is read for which there is no transition from the current state of the automaton) then the sequence is not acceptable (a syntax analyser, e.g. compiler, would generate an error message in this case). The diagram may be completed by adding transitions that would read such invalid input symbols, and these transitions could go to an added "error" state from which all transitions go back to this same state (this error state would be non-accepting). - Figures below: acceptor automata for real numbers

The language "Even-a": We consider the language over the alphabet {a, b, c, d}which consists of all sequences that contain an even number of "a" symbols and no "d" symbol. This is an acceptor automaton for this language:

Equivalence

Definition: Two automata are equivalent if they accept the same language. (Note: this definition is very similar to the equivalence of grammars).

Example of two equivalent FSA:

Implementing FSA

An FSA is an efficient analyser to determine whether a given string is part of the language accepted by the FSA. Note that in each state of the FSA, the next symbol read determines directly the next transition to be executed; one says that the FSA is deterministic. Therefore, complexity of the analysis algorithm is O(n) where n is the length of the input sequence (there is one transition executed per input symbol). So, how can a real implementation of an FSA be obtained ? - Here are several strategies:

• Define the FSA in the notation of a UML or SDL tool and use the tool to generate implementation code.
• Define the FSA as an algorithm in a high-level programming language, e.g. Java. There are two strategies:
  • Reflect the structure of the FSA states and transitions in the control-flow structure of the program
    • See below (on the left) an example of a Java program using this strategy for the Even-a language.
  • Write a program that interprets a transition table. The transition table contains for each state of the FSA and each possible input symbol, what the next state of the FSA is.
    • Such an implementation for the the Even-a language is shown below (on the right). A two-dimensional table contains for each state and each input the next state of the automaton; then an interpretive algorithm (independent of the control flow of the automaton) is used to realize the transitions of the automaton based on the current state, the input read and the information in the table. A sketch of the program is given below (where the function move represents the table).

On the construction of lexical analysers

An automaton is a good tool for lexical analysis (assuming that the lexical rules correspond to the properties of the automaton), but one problem remains: How does one know at what position in the given input string the current lexeme ends and the next one starts ? - Note that in natural languages, it is usually the space character that provides this separation, but in a program, one may have "abc=23+a" without any space.

The solution that is normally adopted is as follows: The lexical rules are defined such that the lexical analyser can always try to find the longest lexeme that can be recognized from the given starting point. In the above example, "abc" will be an identifier, not three identifiers; but "abc=" is not an identifier. It is therefore always necessary to read the next character in order to determine whether it can be part of the current lexeme, or whether the current lexeme must be terminated at this point and the next character will start a new lexeme. In the latter case, it is therefore necessary (in a sense) to return the last read character back to the input string, since it can not be used for the current lexeme which is formed.

In the following example, this returning back of the last character is indicated by "B"; the automaton recognizes three lexemes, namely: real numbers including a decimal point (real), the multiplication operator (mult), and the exponentiation operator (exp). An accepting state (thick cercle) with no further transition indicates that a maximal lexeme has been recognized (return to the calling program). A state labelled E indicates that a lexical error occurred (in this example, a number larger or equal to 1 should not start with a 0 digit; that is, the string "01.0" is invalid; and each number should have a decimal point). The following diagram shows the behavior of the automaton.

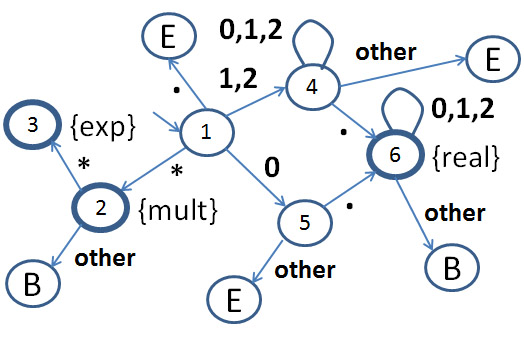
The following transition table for the automaton above shows for each state (row number) and each input received (column) some information about the behavior of the automaton in that case. This information has two parts. The first part indicates the action to be performed; the possible cases are: normal transition (next, next state); an error situation (error, ); a simple return of a lexeme (return, lexeme); and return of a lexeme and turn back the last input (back, lexeme).

Here is a Java program that implements a lexical analyser for this simple example which uses the above transition table.

Some comments on compiler generators

A compiler generator is a program that generates the source code of a compiler from the given definition of the lexical and syntax rules of the programming language which the compiler should process. How to define these rules and how to build such generators was a popular research topic during the 1970ies. One set of tools became later quite popular because they became part of the Unix environment, namely Yacc and Lex. Yacc builds syntax analysers and Lex builds lexical analysers. These tool facilitate the construction of those parts of a compiler that look after lexical and syntax analysis, however, for the part that is responsible for the generation of the object code, there is usually very little support.

The following diagram shows the steps for using a compiler generator (here, it is Lex):

1. the definition of the lexical (or syntax) rules is translated by the compiler generator into a program written in the implementation language of the compiler;
2. the result of Step (1) is translated by the compiler of the implementation language into a language executable by the computer; and
3. the result of Step (2), that is, the generated compiler, is executed on the computer to analyse a program written in the language defined by the rules given under Step (1).

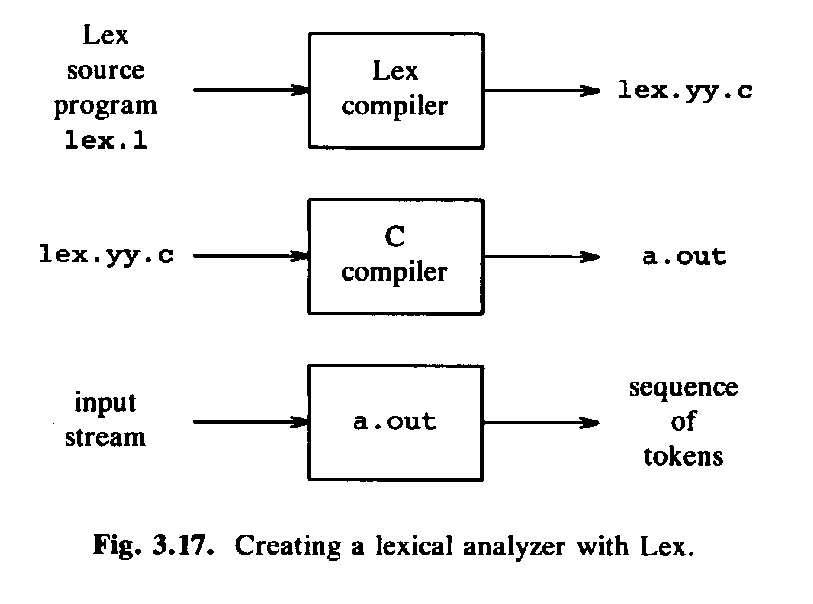
Lex generates a lexical analyser, written in the C language (to be incorporated as part of a compiler) from the definition of the lexical rules given in the form of a variant of regular expressions, sometimes called "regex", with many extensions over the basic operators of concatenation, union and star. There are different variants of "regex" notations used by different tools, such as the Unix tool grep, the pattern class in Java, or the facilities of the Perl and Ruby languages.

The input language used by the tool Lex for the description of regular expressions allows certain variations from the standard basic convention of regular expressions. In particular, several lexical categories may be defined, each by a separate regular expression. The concept of "regular definition" (see above) is supported.

In the following, we want to understand some principles about how a tool like Lex generates a program that does the lexical analysis based on a given set of regular expressions that define the different lexical units of a language. The principle is to derive an accepting automaton that accepts the sequences defined by a regular expression. As seen above, a deterministic automaton can be easily implemented in any programming language. Therefore we want to find a way to obtain a deterministic accepting automaton that accepts exactly the language defined by a given regular expression. However, there is a problem: a regular expression leads naturally to a non-deterministic automaton. Since a non-deterministic automaton does not have an efficient implementation, we have to understand how we can obtain a deterministic automaton that is equivalent to a given non-deterministic one. All this will be discussed in the remainder of this chapter.

Deterministic and non-deterministic automata - this is the same concept as already discussed for LTS

Introduction

In the following, we consider the following problem: Given a regular expression that defines a regular language, we would like to find an automaton that accepts exactly this language. Take for instance the example expression (ab)* ac, that is, the language of all sequences that have zero or more times "a b" and terminated by "a c". Using our intuition to translate the regular expression into an equivalent automaton (an automaton that accepts the same language as defined by the regular expression), we may propose the following automaton:

Unfortunately, this automaton is non-deterministic (it has two "a" transitions from the initial state). Therefore its direct implementation would require some backtracking to determine whether a given input sequence is acceptable. And this has in general high complexity.

We will study in this sub-section the following two questions:

• How can be find a (possibly nondeterministic) automaton that accepts the same language as defined by a given regular expression ?
• How can we find a deterministic automaton equivalent to a given nondeterministic automaton ?
• Note: Solutions to both of these problems allows us to find a deterministic automaton (and an efficient lexical analyser) for a regular language defined by a given regular expression.

Definitions: Nondeterministic accepting automata

Definition: An accepting automaton is deterministic if for each state and each given input symbol, there is at most one possible transition. (Note: when there is no transition for a given input symbol, this means that this symbol can not be accepted in this state).

Definition: An accepting automaton is nondeterministic if for some state and some given input symbol, there are several transitions to different states, or if the automaton contains a spontaneous transition, which is a transition that may occur without reading any input. Note: A spontaneous transition is usually labelled є (meaning that it reads the empty input string).

Definition: A sequence of sympols is accepted by a nondeterministic automaton if the automaton allows for (at least) one sequence of executed transitions that reads the input sequence and arrives finally at an accepting state.

Reminder: Definition: Two automata are equivalent if they accept the same language.

Note: Although the definition of a non-deterministic automaton is nearly identical to the definition of an LTS, there is an important difference in using them. LTS are normally models of state machines that can make non-deterministic choices (and only one execution path will be considered at a given time), while for nondeterministic automata, all possible execution paths will be explored in parallel in order to see whether a given sequence of symbols can be accepted.

Example (a)

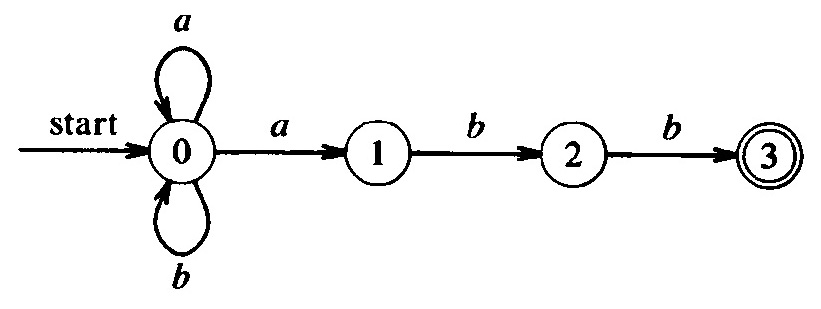
Below is the diagram of a nondeterministic automaton that accepts the language defined by the regular expression (a | b)* a b b .

Tansition table:

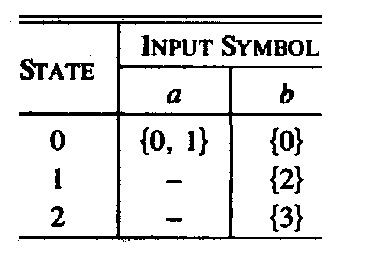
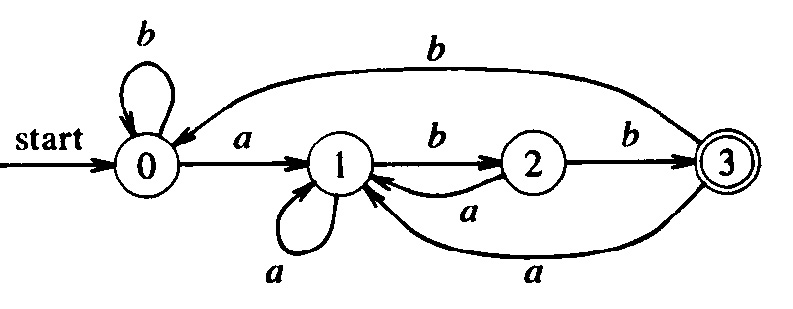
This automaton is equivalent to the deterministic automaton below (which accepts the same language). Note: You see that the structure of the nondeterministic automaton is simpler; it corresponds directly to the structure of the regular expression.

Example (b)

The diagram below defines a nondeterministic automaton that accepts the language defined by the regular expression   a a*  |  b b* .

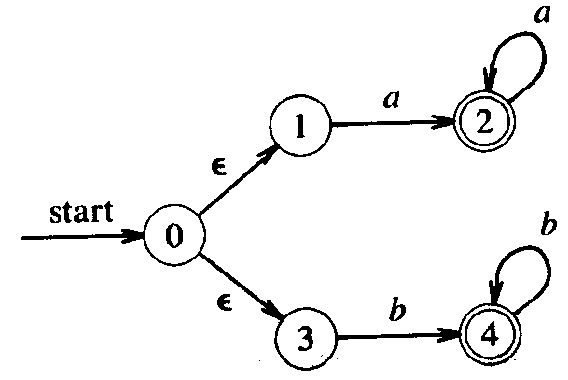
The nondeterministic automata are in general not very efficient for performing lexical analysis (in contrast to the deterministic automata, see above). They have to explore the different possible execution paths to see if one of them is able to accept the given input string. Nevertheless, the non-deterministic automata are more apt at representing certain languages; for instance, in the case of Example (a) above, the structure of the non-deterministic automaton corresponds directly to the regular expression  (a | b)* a b b, while this correspondence is difficult to see for the equivalent deterministic automaton.

How can one find a deterministic automaton that is equivalent to a given non-deterministic automaton ?

The idea of the conversion algorithm (well-known in computer science and explained in the book by Aho) is to consider the processing of an input string by the given non-deterministic automaton by exploring all possible execution paths in parallel. While a deterministic automaton, after having analysed the given input string up to a certain point, is in a specific state, a non-deterministic automaton could in general be in several states (depending on the transition path that has been executed up to this point); these states form a subset of the total set of states of the automaton. In a sense, the algorithm of constructing the equivalent deterministic automaton performs (during design time) all the transitions that the nondeterministic automaton may perform during the analysis of any given input sequence.

Given a nondeterministic automaton N and an equivalent deterministic automaton D to be constructed. We start from the initial state (when no input symbol has been read). N may be in any state reachable from its intial state by spontaneous transitions. This set corresponds to the intial state of D. Let us assume that some prefix of the input has already been read and x is the next input symbol. N could be in a subset of its states, this subset corresponds to the state in which D would be (it is in a spefic state, since it is deterministic). If N has a transition reading x from any of its possible states, then D should have a transition reading x from its current state. After reading x, N could be in any state reached from one of its current states by reading x (if that is possible) and then doing spontaneous transitions. This set of states corresponds to the state in which D would be after reading x. And so on. If at the end of the analysis one of the states reached by N is accepting, then the state reached by D is accepting.

We conclude therefore that an equivalent deterministic automaton D can be constructed from a given non-deterministic automaton N as follows:

• A state of D corresponds to a subset {s₁, s₂, ... s_k} of states of N.

• The initial state of D is the subset of states of N that can be reached from N's initial state by spontaneous transitions only.
• A transition in D from a state {s₁, s₂, ... s_k} with input z leads to the next state {s₁', s₂', ... s_k''} where the latter subset contains all states of N that can be reached from some state of the subset {s₁, s₂, ... s_k} by following a transition accepting z, and also those states that can be reached from the latter by executing spontaneous transitions only.
• A state {s₁, s₂, ... s_k} is accepting if one of the states in this subset is an accepting state in N.

A systematic algorithm for constructing an equivalent deterministic automaton uses the following (mathematical) functions:

• The function є-closure(s), for a given nondeterministic automaton N, determines the subset of states of N that can be reached from state s by using spontaneous transitions only.

• The function є-closure(S), for a given nondeterministic automaton N, determines, for a given subset S of states of N, what are the states of N that can be reached from any state in S by using spontenous transitions only.
• The function move(S, a) , for a given nondeterministic automaton N, determines which subset of states of N can be reached from any state in S by a single transition consuming the input a.

Here are some algorithms for these functions (similar algorithms are given in the book by Aho):

move(S, a) = {s' ׀ exists s in S and there is a transition from s to s' consuming a}

Algorithm for calculating є-closure(S):
        Closure = S; Temp = S;
        while (Temp != empty) {
                s = get-some-element(Temp);
                for each spontaneous transition from s to s' {
                        if (s' is not in Closure) {add s' to Closure and to Temp}
                } }

And here is an algorithm to construct the table of transitions for a deterministic automaton D that is equivalent to a given non-deterministic automaton N. Note: Dstates is a subset of the states of D, that is, a set of set of states of N. At the end of the algorithm, itcontains all the states of D, and Dtran[T, a] is the next state of D from the state T with input a. See also Algorithm 3.2 in the book by Aho.

In (relatively simple) examples considered in this course, one can obain the equivalent deterministic automaton simply by drawing its state diagram by exploring all its states (from its initial state) as indicated by the above algorithm. An unmarked state simply means that the possible transitions from it should be explored.

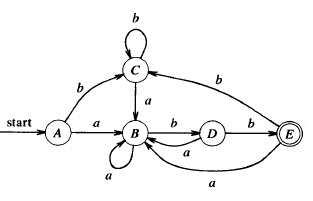
Here is an example. The nondeterministic automaton below (left) is equivalent to the deterministic automaton on the right. It is also equivalent to the regular expression ((b c  +  a ) c )* a

Note: the equivalent minimal deterministic automaton is the following (see text below)

How to find a (non-deterministric) automaton that accepts the language defined by a given regular expression

An algorithm for finding a non-deterministic automaton that accepts the language defined by a given regular expression is described in the book by Aho (Algorithm 3.3). The principle is very simple: For each constructor (operator) of regular expressions one defines how an automaton corresponding to the constructed regular expression can be built from the automata representing the sub-expressions of the regular expression. Then these constructions are applied in the order corresponding to the structure of the given regular expression. For example, let us consider the expression e = s | t  where the automata corresponding to the subexpressions s and t are already found; assume that they are called N(s) and N(t), respectively. Then it is clear that the diagram below represents a (non-deterministic) automaton that accepts the language defined by e. (Note that the circle on the left side of the automaton that represents N(s) is its initial state, and the circle on the right represents its only accepting state. All the construction rules assure that the automata corresponding to sub-expressions have a single accepting state.)

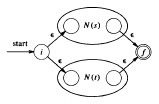
For more details about the construction rules for the other regular expresssion operators, see Algorithm 3.3. There you can also find the complete example of the regular expression (a | b)* a b b.

Minimal automata and equivalence

Let us consider the example of the regular expression (a | b)* a b b . If we apply the automata construction algorithm, followed by the automata determination algorithm, we get the automaton shown below, which is different from the deterministic automaton given for Example (a) above. Actually, these two automata are equivalent; they accept the same language. However, they are not identical automata (in the sense that there is no bi-directional correspondence between their states and transitions; note that the names given to states have no significance), since they have different numbers of states.

Definition: A deterministic automaton is minimal if there exist no equivalent deterministic automaton that has fewer states.

If there are several equivalent automata, we may ask the question: Which of these automata is more interesting ? - One possible answer to this question is to say: the one that is simpler. But how would you measure simplicity for an automaton ? - Two possible answers come to mind: (1) the one with less states, and (2) the one with less transitions. One normally opts for answer (1) and looks for automata with a small number of states. Among all equivalent automata, one that has the least number of states is called minimal. Algorithms for finding a minimal automaton equivalent to a given automaton are known. Such an algorithm could be applied to the automaton above in order to obtain the deterministic automaton shown with Example (a). Note: The LTSA tool can be used to find the minimal automaton for a given deterministic automaton (see example "accepting automata minimization.lts")

Question: How can one verify that a given automaton is minimal ? - Answer: If the language accepted by each state of the automaton (taken as initial state) is different from the languages accepted by the other states, then the automaton is minimal. Inversely, if one finds that two states of the automata (when taken as initial states) accept the same language, then these states can be combined into a single state in order to form an equivalent automaton with less states. In the example above, state A and C are equivalent and can be combined.

Created: January 29, 2008, last revision: February 23, 2015