Area: Distributed computing, distributed algorithms, cellular automata.

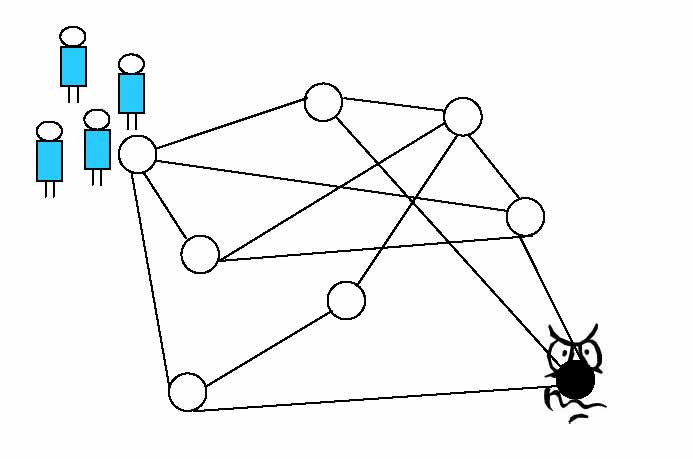Black Holes: Locating harmful hosts

In current and future networked environments supporting mobile software agents, a pressing security problem is the problem of protecting the agents from host attacks (i.e., harmful processes stored at visited sites). In this project we are concerned with the problem of operating in an environment that contains highly harmful items, located at some nodes, which destroy any incoming agents. We are interested in constructing software agents capable, as a team, to unambiguously and with as few losses as possible determine the location of the harmful items; a rescue activity can then take place once the location phase has been completed.

Some References

P. Flocchini, D. Ilcinkas, N. Santoro.
Ping pong in dangerous graphs: optimal black hole search with pure tokens (extended version of DISC 2008 ).

S. Dobrev, P. Flocchini, G. Prencipe, N. Santoro
Mobile search for a black hole in an anonymous ring. Algorithmica, 48(1): 67-90, 2007.

S. Dobrev, P. Flocchini, G. Prencipe, N. Santoro
Searching for a Black Hole in Arbitrary Networks: Optimal Mobile Agent Protocols. Distributed Computing, 19(1), 1-19, 2006.

S. Dobrev, P. Flocchini, R. Kralovic, G. Prencipe, P. Ruzicka, N. Santoro
Black hole search in common interconnection networks , Networks , vol 47(2), 61-71, 2006.

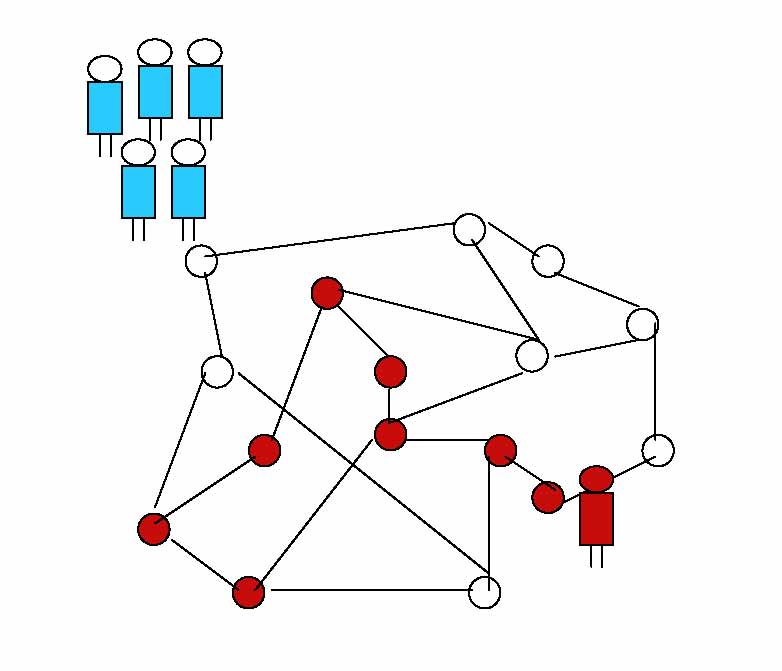Intruder Capture

An intruder is an alien process that moves on the network to sites unoccupied by the system's agents. The concern for the severe damage intruders can cause has motivated a large amount of research, especially on detection. Once the presence of an intruder is detected, a team of system agents should be deployed to neutralize it (i.e., to surround it occupying all the neighbours of the site where it currently resides). In this project we are interested in designing strategies for the agents to surround the intruder.

Some References

L. Barriere, P. Flocchini, F. V. Fomin, P. Fraigniaud, N. Nisse, N. Santoro, D.M. Thilikos.
Connected Graph Searching, Information and Computation, 219: 1-16, 2012.

P. Flocchini.
Contamination and decontamination in majority-based systems, Journal of Cellular Automata, 4(3):183-200, 2009.

P. Flocchini, B. Mans, N. Santoro.
Tree Decontamination with Temporary Immunity, 330-341, ISAAC 2008.

P. Flocchini, M.J. Huang, F.L. Luccio.
Decontamination of hypercubes by mobile agents, Networks, 52(3): 167-178, 2008.

P. Flocchini, F.L. Luccio, M. Huang
Decontamination of chordal rings and tori using mobile agents. International Journal of Foundation of Computer Science, 18(3), 547-564, 2007.

L. Barriere, P. Flocchini, P. Fraigniaud, N. Santoro
Can we elect if we cannot compare ? , Proc. of 15th ACM Symposium on Parallel Algorithms and Architectures (SPAA20003).

Mobile Robots

The problem is to coordinate a set of autonomous, mobile robots in the plane under different assumptions on their capabilities. A robot can observe the positions of the other robots and can move accordingly towards its goal. Each time a robot observes the environment, however, it forgets what it had seen before (i.e., robots are oblivious). In spite of all these weaknesses, several useful tasks can be succesfully accomplished. Among others, some of the issues of interest are:

• Algorithms for pattern formation (e.g., the robots must place themselves on a circle)
• Algorithms for reaching an agreement
• Faulty situations or inaccurate information
• Limited visibility versus total visibility

Some References

G.A. Di Luna, P. Flocchini, S.G. Chaudhuri, F. Poloni, N. Santoro, G. Viglietta.
Mutual visibility by luminous robots without collisions. Information and Computation, in press.

S. Das, P. Flocchini, G. Prencipe, N. Santoro, M. Yamashita.
Autonomous mobile robots with lights Theoretical Computer Science, 609: 171-184, 2016.

S. Das, P. Flocchini, G. Prencipe, N. Santoro, M. Yamashita.
Forming Sequences of Geometric Patterns with Oblivious Mobile Robots. Distributed Computing, 28(2): 131-145, 2015.

P. Flocchini.
Computations by Luminous Robots. 14th International Conference on Ad-hoc, Mobile, and Wireless Networks, (ADHOC-NOW), 238-252, 2015.

M. Cieliebak, P. Flocchini, G. Prencipe, N. Santoro.
Distributed Computing by Mobile Robots: Gathering, SIAM Journal on Computing, 41(4): 829-879, 2012.

P. Flocchini, G. Prencipe, N. Santoro, P. Widmayer.
Arbitrary pattern formation by asynchronous, anonymous, oblivious robots, Theoretical Computer Science, vol. 407, number 1-3, 412--447, 2008.

P. Flocchini, G. Prencipe, N. Santoro
Self-deployment of mobile sensors on a ring, Theoretical Computer Science, 402(1): 67-80, 2008.

P. Flocchini, G. Prencipe, N. Santoro, P. Widmayer
Gathering of asynchronous mobile robots with limited visibility, Theoretical Computer Science , vol 337: 1-3, 147-168, 2005.

Continuous Cellular Automata

Fuzzy Cellular Automata (FCA) are continuous generalizations of Boolean cellular automata where the states of the cells are real values. The local transition rule of a FCA is the ``fuzzification" of the disjunctive normal form that describes the local function of the corresponding Boolean cellular automata. Fuzzy Cellular Automata are very interesting discrete time dynamical systems and they have been employed and studied in various context. This project is concerned with the study of their properties.

Some References

H. Betel, P. Flocchini.
On the relationship between fuzzy and Boolean cellular automata, Theoretical Computer Science, 412(8-10): 703-713, 2011.

H. Betel, P. Flocchini.
On the asymptotic behaviour of circular fuzzy cellular automata, Journal of Cellular Automata, 6:1, 25-52, 2011.

P. Flocchini, V. Cezar
Radial View of Circular Fuzzy Cellular Automata , Fundamenta Informaticae , vol. 87(3), 165-183, 2008.

P. Flocchini, F. Geurts, A. Mingarelli, N. Santoro
Convergence and Aperiodicity in Fuzzy Cellular Automata: Revisiting Rule 90, Physica D, vol. 142, 20-28, 2000.

Sense of Direction

Sense of Direction is a property of labeled graphs which has been shown to have a definite impact on computability and complexity in systems of communicating entities, and whose applicability ranges from the analysis of graph classes to distributed object systems.

• Naming schemes based on sense of direction.
• Distributed algorithms and sense of direction
• Impact of sense of direction on computability.
• Graph symmetries and sense of direction.
• Sense of direction in wireless systems.

Some References

L. Barriere, P. Flocchini, P. Fraigniaud, N. Santoro
Rendezvous and Election of Mobile Agents: Impact of Sense of Direction, Theory of Computing Systems, 40(2), 143-162, 2007.

P. Flocchini, B. Mans, N. Santoro
Sense of direction in distributed computing , Theoretical Computer Science, vol. 291, 29-53, 2003.

P. Flocchini, A. Roncato, N. Santoro
Sense of direction and backward consistency in advanced distributed systems , SIAM Journal on Computing , vol. 32:2, 281-306, 2003.

P. Flocchini, B. Mans, N. Santoro.
On the Impact of Sense of Direction on Message Complexity , Information Processing Letters, vol. 63, 23-31,1997.

P. Flocchini
Minimal Sense of Direction in Regular Networks , Information Processing Letters, vol. 61, 331-338, 1997.

P. Flocchini, B. Mans
Optimal election in labeled hypercubes , Journal of Parallel and Distributed Computing, vol. 33, n. 1, 76-83, 1996.

P. Flocchini, N. Santoro
Topological Constraints for Sense of Direction International Journal of Foundations of Computer Science, 9(2), p. 179-198, 1998.

• Sense of Direction HOME PAGE

Dynamos

Let G be a simple connected graph where every node is colored either black or white. Consider now the following repetitive process on G: each node recolors itself, at each local time step, with the color held by the majority of its neighbors. Depending on the initial assignment of colors to the nodes and on the definition of majority, different dynamics can occur. In the context of distributed computing, this repetitive process is particularly important in that it describes the impact that a set of initial faults can have in majority-based systems (where black nodes correspond to faulty elements and white to non-faulty ones). A dynamo (dynamic monopoly) is a pattern which converges to a monochromatic situation under the majority rule.

• Study of lower and upper bounds on the size of dynamos on specific topologies.
• Study of trade-offs time/size.
• Study of different models.

Some References

P. Flocchini, E. Lodi, F. Luccio, L. Pagli, N. Santoro
Dynamic Monopolies in Tori, Discrete Applied Mathematics , 2003.

Flocchini, R. Kralovic, A. Roncato, P. Ruzicka, N. Santoro
On time versus size for monotone dynamic monopolies in regular topologies , Journal of Discrete Algorithms, 135-156, vol. 2 (2), 2002.

P. Flocchini, F. Geurts, N. Santoro
Irreversible dynamos in chordal rings , Discrete Applied Mathematics, vol.112, 23-42, 2001.