



The block diagram for the demosaicking of the stripe structure is the following:
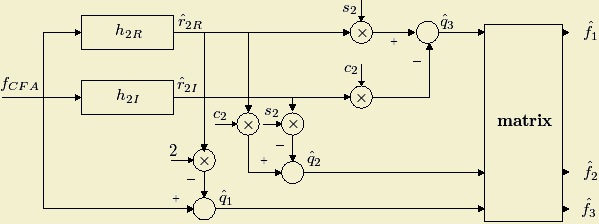
By tracing the demosaicking steps described in the figure and omitting any multiplications involving a constant operand, the number of multiplications S required to demosaic one image pixel is:
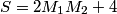
Where both the real and the imaginary parts of the h2 filter have a M1xM2 order.
Because of the diagonal symmetry we noticed in the power spectrum we only took into consideration the square filters when performing the greedy algorithm. In this case:
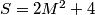
The number of multiplications used by the algorithm can be reduced if we take into consideration filter properties. If we make use of the filter quadrantal symmetry, the number of multiplications required to demosaic one pixel is:
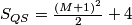
If we use separable filters, then the number of computations required for demosaicking becomes:
The filter design training set and the demosaicking test set of color images consisted of subsets from the 24 Kodak photo-sampler images of size 512x768 that are widely used in the demosaicking literature. The figures below show the changes to objective demosaicking quality, measured by CMSE as a function of computational complexity, measured by the number of multiplications for the general structure without imposing quadrantal symmetry.
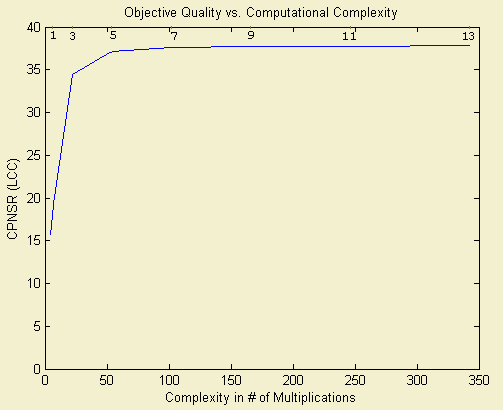
The experiment results confirm the tradeoff relationship between demosaicking quality and speed. The plot line indicates that a 5x5 filter size represents a good filter order when demosaicking a Stripe CFA image.