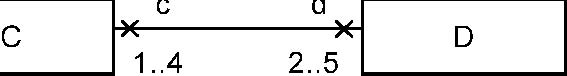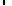7.3.3 Association
An association describes a set of tuples whose values refer to typed instances. An instance of an association is called a
link.
*Generalizations
*Description
An association specifies a semantic relationship that can occur between typed instances. It has at least two ends represented
by properties, each of which is connected to the type of the end. More than one end of the association may have the same type.
An end property of an association that is owned by an end class or that is a navigable owned end of the association indicates
that the association is navigable from the opposite ends, otherwise the association is not navigable from the opposite ends.
*Attributes
• isDerived : Boolean Specifies whether the association is derived from other model elements such as other associations or
constraints. The default value is false.
*Associations
• navigableOwnedEnd : Property [*] The navigable ends that are owned by the association itself. Subsets Association::ownedEnd.
• / endType: Type [1..*] References the classifiers that are used as types of the ends of the association.
•
memberEnd : Property [2..*] Each end represents participation of instances of the classifier connected to the end in links
of the association. This is an ordered association. Subsets Namespace ::member.
• ownedEnd : Property [*] The ends that are owned by the association itself. This is an ordered association. Subsets Association::memberEnd,
Classifier::feature, and Namespace ::ownedMember.
*Constraints
[1] An association specializing another association has the same number of ends as the other association.
self.parents()->forAll(p | p.memberEnd.size() = self.memberEnd.size())
[2] When an association specializes another association, every end of the specific association corresponds to an end of the
general association, and the specific end reaches the same type or a subtype of the more general end.
[3] endType is derived from the types of the member ends.
self.endType = self.memberEnd->collect(e | e.type)
[4] Only binary associations can be aggregations.
self.memberEnd->exists(aggregation <> Aggregation::none) implies self.memberEnd->size() = 2
[5] Association ends of associations with more than two ends must be owned by the association.
if memberEnd->size() > 2 then ownedEnd->includesAll(memberEnd)
*Semantics
An association declares that there can be links between instances of the associated types. A link is a tuple with one value
for each end of the association, where each value is an instance of the type of the end.
When one or more ends of the association have isUnique=false, it is possible to have several links associating the same set
of instances. In such a case, links carry an additional identifier apart from their end values.
When one or more ends of the association are ordered, links carry ordering information in addition to their end values.
For an association with N ends, choose any N-1 ends and associate specific instances with those ends. Then the collection
of links of the association that refer to these specific instances will identify a collection of instances at the other end.
The multiplicity of the association end constrains the size of this collection. If the end is marked as ordered, this collection
will be ordered. If the end is marked as unique, this collection is a set; otherwise it allows duplicate elements.
Issue 8088 - Clarify subsetting.
Subsetting represents the familiar set-theoretic concept. It is applicable to the collections represented by association ends,
not to the association itself. It means that the subsetting association end is a collection that is either equal to the collection
that it is subsetting or a proper subset of that collection. (Proper subsetting implies that the superset is not empty and
that the subset has fewer members.) Subsetting is a relationship in the domain of extensional semantics.
Specialization is, in contrast to subsetting, a relationship in the domain of intentional semantics, which is to say it characterized
the criteria whereby membership in the collection is defined, not by the membership. One classifier may specialize another
by adding or redefining features; a set cannot specialize another set. A naïve but popular and useful view has it that as
the classifier becomes more specialized, the extent of the collection(s) of classified objects narrows. In the case of associations,
subsetting ends, according to this view, correlates positively with specializing the association. This view falls down because
it ignores the case of classifiers which, for whatever reason, denote the empty set. Adding new criteria for membership does
not narrow the extent if the classifier already has a null denotation.
Redefinition is a relationship between features of classifiers within a specialization hierarchy. Redefinition may be used
to change the definition of a feature, and thereby introduce a specialized classifier in place of the original featuring classifier,
but this usage is incidental. The difference in domain (that redefinition applies to features) differentiates redefinition
from specialization.
Issue 8088 - Clarify subsetting.
Note – For n-ary associations, the lower multiplicity of an end is typically 0. A lower multiplicity for an end of an n-ary
association of 1 (or more) implies that one link (or more) must exist for every possible combination of values for the other
ends.
Issue 8015 - Clarify transitivity in composition.
An association may represent a composite aggregation (i.e., a whole/part relationship). Only binary associations can be aggregations.
Composite aggregation is a strong form of aggregation that requires a part instance be included in at most one composite at
a time. If a composite is deleted, all of its parts are normally deleted with it. Note that a part can (where allowed) be
removed from a composite before the composite is deleted, and thus not be deleted as part of the composite. Compositions may
be linked in a directed acyclic graph with transitive deletion characteristics; that is, deleting an element in one part of
the graph will also result in the deletion of all elements of the subgraph below that element. Composition is represented
by the isComposite attribute on the part end of the association being set to true.
Issue 8963 - clarify meaning of navigability
Navigability means instances participating in links at runtime (instances of an association) can be accessed efficiently from
instances participating in links at the other ends of the association. The precise mechanism by which such access is achieved
is implementation specific. If an end is not navigable, access from the other ends may or may not be possible, and if it is,
it might not be efficient. Note that tools operating on UML models are not prevented from navigating associations from non-navigable
ends
*Semantic Variation Points
• The logical relationship between the derivation of an association and the derivation of its ends is not defined.
• The interaction of association specialization with association end redefinition and subsetting is not defined.
*Notation
Any association may be drawn as a diamond (larger than a terminator on a line) with a solid line for each association end
connecting the diamond to the classifier that is the end’s type. An association with more than two ends can only be drawn
this way.
A binary association is normally drawn as a solid line connecting two classifiers, or a solid line connecting a single classifier
to itself (the two ends are distinct). A line may consist of one or more connected segments. The individual segments of the
line itself have no semantic significance, but they may be graphically meaningful to a tool in dragging or resizing an association
symbol.
An association symbol may be adorned as follows:
• The association’s name can be shown as a name string near the association symbol, but not near enough to an end to be confused
with the end’s name.
• A slash appearing in front of the name of an association, or in place of the name if no name is shown, marks the association
as being derived.
• A property string may be placed near the association symbol, but far enough from any end to not be confused with a
property string on an end.
Issue 8066 - Clarify meaning of arrow symbol on binary association.
On a binary association drawn as a solid line, a solid triangular arrowhead next to or in place of the name of the association
and pointing along the line in the direction of one end indicates that end to be the last in the order of the ends of the
association. The arrow indicates that the association is to be read as associating the end away from the direction of the
arrow with the end to which the arrow is pointing (see Figure 7.21). This notation is for documentation purposes only and
has no general semantic interpretation. It is used to capture some application-specific detail of the relationship between
the associated classifiers.
• Generalizations between associations can be shown using a generalization arrow between the association symbols.
An association end is the connection between the line depicting an association and the icon (often a box) depicting the connected
classifier. A name string may be placed near the end of the line to show the name of the association end. The name is optional
and suppressible.
Various other notations can be placed near the end of the line as follows:
• A property string enclosed in curly braces. The following property strings can be applied to an association end:
• {subsets <property-name>} to show that the end is a subset of the property called <property-name>.
Issue 8204 - change ‘redefined’ to ‘redefines’
• {bag} to show that the end represents a collection that permits the same element to appear more than once.
• If the end is navigable, any property strings that apply to an attribute.
Note that by default an association end represents a set.
An open arrowhead on the end of an association indicates the end is navigable. A small x on the end of an association indicates
the end is not navigable. A visibility symbol can be added as an adornment on a navigable end to show the end’s visibility
as an attribute of the featuring classifier.
If the association end is derived, this may be shown by putting a slash in front of the name, or in place of the name if no
name is shown.
The notation for an attribute can be applied to a navigable end name as specified in the Notation subsection of Property
(from Kernel , AssociationClasses ) on page 125.
An association with aggregationKind = shared differs in notation from binary associations in adding a hollow diamond as a
terminal adornment at the aggregate end of the association line. The diamond shall be noticeably smaller than the diamond
notation for associations. An association with aggregationKind = composite likewise has a diamond at the aggregate end, but
differs in having the diamond filled in.
Issue 8956 - add explanation for the notation for association end ownership
Ownership of association ends by an associated Classifier may be indicated graphically by a small filled circle, which for
brevity we will term a dot. The dot is to be drawn integral to the graphic path of the line, at the point where it meets
the classifier, inserted between the end of the line and the side of the node representing the Classifier. The diameter of
the dot shall not exceed half the height of the aggregation diamond, and shall be larger than the width of the line. This
avoids visual confusion with the filled diamond notation while ensuring that it can be distinguished from the line.
This standard does not mandate the use of explicit end-ownership notation, but defines a notation which shall apply in models
where such use is elected. The dot notation must be applied at the level of complete associations or higher, so that the absence
of the dot signifies ownership by the association. Stated otherwise, when applying this notation to a binary association
in a user model, the dot will be omitted only for ends which are not owned by a classifier. In this way, in contexts where
the notation is used, the absence of the dot on certain ends does not leave the ownership of those ends ambiguous.
This notation may only be used on association ends which may, consistent with the metamodel, be owned by classifiers. Users
may conceptualize the dot as showing that the model includes a property of the type represented by the classifier touched
by the dot. This property is owned by the classifier at the other end.
The dot may be used in combination with the other graphic line-path notations for properties of associations and association
ends. These include aggregation type and navigability.
The dot is illustrated in Figure 7.19, at the maximum allowed size. The diagram shows endA to be owned by classifier B, and
because of the rule requiring the notation be applied at the level of complete associations (or above), this diagram also
shows unambiguously that end B is owned by BinaryAssociationAB.
 Figure 7.19 - Graphic notation indicating exactly one association end owned by the association
Figure 7.19 - Graphic notation indicating exactly one association end owned by the association
Navigability notation was often used in the past according to an informal convention, whereby non-navigable ends were assumed
to be owned by the association whereas navigable ends were assumed to be owned by the classifier at the opposite end. This
convention is now deprecated.
Aggregation type, navigability, and end ownership are orthogonal concepts, each with their own explicit notation. The notational
standard now provides for combining these notations as shown in Figure 7.20, where the associated nodes use the default rectangular
notation for Classifiers. The dot is outside the perimeter of the rectangle. If non-rectangular notations represent the
associated Classifiers, the rule is to put the dot just outside the boundary of the node.


Figure 7.20 - Combining line path graphics
*Presentation Options
When two lines cross, the crossing may optionally be shown with a small semicircular jog to indicate that the lines do not
intersect (as in electrical circuit diagrams).
Various options may be chosen for showing navigation arrows on a diagram. In practice, it is often convenient to suppress
some of the arrows and crosses and just show exceptional situations:
• Suppress all arrows and x’s. No inference can be drawn about navigation. This is similar to any situation in which information
is suppressed from a view.
• Suppress arrows for associations with navigability in both directions, and show arrows only for associations with one-way
navigability. In this case, the two-way navigability cannot be distinguished from situations where there is no navigation
at all; however, the latter case occurs rarely in practice.
If there are two or more aggregations to the same aggregate, they may be drawn as a tree by merging the aggregation ends into
a single segment. Any adornments on that single segment apply to all of the aggregation ends.
*Style Guidelines
Lines may be drawn using various styles, including orthogonal segments, oblique segments, and curved segments. The choice
of a particular set of line styles is a user choice.
Generalizations between associations are best drawn using a different color or line width than what is used for the associations.
*Examples
Figure 7.21 shows a binary association from Player to Year named PlayedInYear.
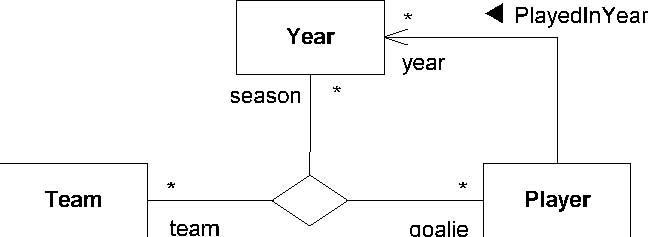
Figure 7.21 - Binary and ternary associations
The solid triangle indicates the order of reading: Player PlayedInYear Year. The figure further shows a ternary association
between Team, Year, and Player with ends named team, season, and goalie respectively.
The following example shows association ends with various adornments.

{subsets b}
Figure 7.22 - Association ends with various adornments
The following adornments are shown on the four association ends in Figure 7.22.
• Names a, b, and d on three of the ends.
• Multiplicities 0..1 on a, * on b, 1 on the unnamed end, and 0..1 on d.
• Subsetting on d. For an instance of class C, the collection d is a subset of the collection b. This is equivalent to the OCL
constraint:
context C inv: b->includesAll(d) The following examples show notation for navigable ends.



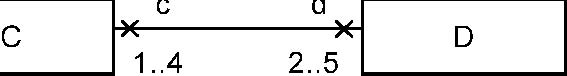







Figure 7.23 - Examples of navigable ends
In Figu
re 7.23
:
• The fifth pair IJ shows a binary association with one end navigable and the other having unspecified navigability.
Figu
re 7.24
shows that the attribute notation can be used for an association end owned by a class, because an association end owned by
a class is also an attribute. This notation may be used in conjunction with the line-arrow notation to make it perfectly clear
that the attribute is also an association end.

Figure 7.24 - Example of attribute notation for navigable end owned by an end class
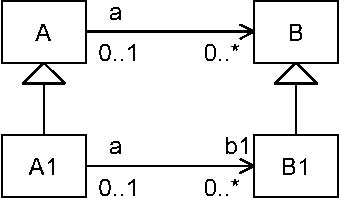
Figure 7.25 shows the notation for a derived union. The attribute A::b is derived by being the strict union of all of the
attributes that subset it. In this case there is just one of these, A1::b1. So for an instance of the class A1, b1 is a subset
of b, and b is derived from b1.
/b {union}
a
{subsets b}
Figure 7.25 - Derived supersets (union)
Figure 7.26 shows the black diamond notation for composite aggregation.
 Figure 7.26 - Composite aggregation is depicted as a black diamond
Figure 7.26 - Composite aggregation is depicted as a black diamond
*Changes from previous UML
AssociationEnd was a metaclass in prior UML, now demoted to a member of Association. The metaatribute targetScope that characterized
AssociationEnd in prior UML is no longer supported. Fundamental changes in the abstract syntax make it impossible to continue
targetScope or replace it by a new metaattribute, or even a standard tag, there being no appropriate model element to tag.
In UML 2, the type of the property determines the nature of the values represented by the members of an Association.