For each node v, a relative position P(v) within its layer has to be
calculated, such that there are only few edge crossings.
Since the hierarchy is proper, the number of crossings c originated by
the edges 
between two adjacent layers 
and 
can
be easily
determined by a plane sweep algorithm [Sa94] in time
.
However, the problem of finding permutations of the sequences 
and 
to
get a minimal number of crossings is 
-complete [GaJo83].
Methods to solve the crossing problem can be found in
[STT81, EaWo86, EaKe86, EaSu90, Sa94, JuMu96].
In practice, the most successful algorithm is the layer-by-layer-sweep:
(2) for each layer
(3) for each
(4) Calculate weight
(5) od
(6) Sort the nodes of
(7) od
(8) for each
(9) od
(1) while the crossing number is not satisfactory do
from i = 1 to n do
do
;
according to the weight ;
from i = n to 1 do ... similar with 
od
The first traversal (line (2)-(7)) is a top down traversal,
the second (line (8)) is a bottom up traversal.
Other variations of this method sweep only top down or only bottom up,
or from the center outwards.
[Sa94] describes a variation with limited backtracking: if a sweep
did not reduce the number of crossings, the old configuration is taken.
The crucial point is the selection of the weights 
and 
.
[STT81] proposes the barycenter weight (P(w) is the relative
position of the node w in the predecessor or successor layer, respectively):
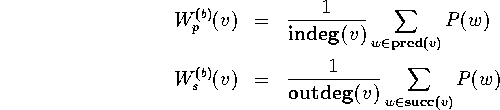
[EaWo86, GKN93] propose the median of the sequence 
of predecessors of a node v:
We also made experiments with combinations of both, using
A method of calculating the optimal permutation of two layers where one
layer is fixed was proposed in [JuMu96].
Assume that the permutation of is fixed, and a permutation of
should be calculated.
Let 
denote the number of crossings among edges adjacent to
in a permutation of where 
.
Let 
if , and 
otherwise.
Then the number of crossings of a permutation of can be described
as
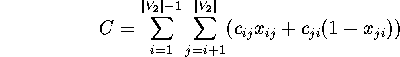
The optimal permutation of can be found by calculating 
such that C is minimal, subject to
(1) 
for 
,
and (2) 
for 
.
The "3-cycle constraints" (1) guarantee that the result describes a valid
permutation.
This linear integer programming problem can be solved by a variation
of the branch and cut algorithm [JuMu96].
This method is suitable up to 
, but it is much too slow
for larger graphs.
Statistical experiments [JuMu96, Sa96b] show that apart from the optimal
method for two layers where one is fixed,
the best heuristic is 
with 
,
followed by 
, and at last by 
.
These methods are also closer to the optimum and faster than various
greedy or stochastic methods described in [EaKe86, JuMu96].
However, this experimental result does not hold if there are more
than two layers, and a layer-by-layer-sweep is used.
Firstly, a sweep with the two-layer-optimal algorithm does not calculate
the optimal crossing number of the whole multi-layer-graph since a nonoptimal
permutation of some adjacent layers might produce less crossings
than a situation where the first layer is optimal, but the other
layers are only optimal derived from the first layer.
Secondly, it is not obvious which of 
and
produces the fewest crossings in a multi-layer-graph:
there are many examples where any of the three is the best.