M. Wand [6] has presented a data structure 
over which the Hoare calculus is
incomplete. From our earlier remarks it follows that is not expressive.
The signature of extends the Boolean signature by
and the operations are defined on the set 
via
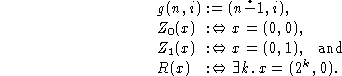
Wand considers the following program 
over :
It is obvious that 
, which is the upper
copy of 
in the figure, so in particular the Hoare triple
is valid.
Assuming that this can be proven in the Hoare calculus, we submit the annotated program to NPPV.
We have to supply the while-loop with an invariant, which, if it exists, must be a logical
expression with at most 
as free variable. NPPV allows us to enter such an ``unknown''
expression, so we enter
{ R(x) }
WHILE not (Z0(x) or Z1(x)) DO { I(x) }
x := g(x)
{ Z0(x) }
NPPV generates the following verification conditions
R(x) => I(x)
I(x) and not (Z0(x) or Z1(x)) => I(g(x))
I(x) and Z1(x) => Z0(x)
from which we conclude that I(x) describes the same set as before, namely
.
Using the Beth-definability theorem[2], Wand shows that the above set is not definable, contradicting the existence of an expression I(x). We shall now give an elementary proof of this result.
