Given an annotated program, i.e. a construct 
, where every while-loop in
C is annotated with an invariant, we could attempt to calculate wlp(C,Q) and check whether
this is implied by P. However, we have seen that wlp(C,Q) need not exist when C contains
a while loop. Even if it did, the resulting logical expression, if not valid, would hardly
give us a clue as to the source of the error.
Therefore we use a ``localized'' approach: First, we replace the wlp-function by the simpler
function pre, defined on annotated programs as
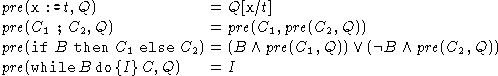
Then we generate a set of simple logical expressions, so called verification conditions :
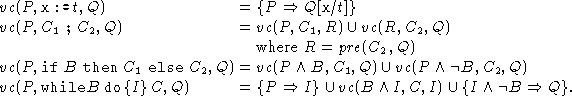
Each verification condition is associated with a certain identifiable place in the program. Verification conditions are propagated through straight line subprograms. If this is not desired, an intermediate assertion {R} can be placed after a semicolon ``;''. In this case we calculate
It can be shown that the given annotated program satisfies its specification if and only if all these verification conditions are valid. More precisely, we have:
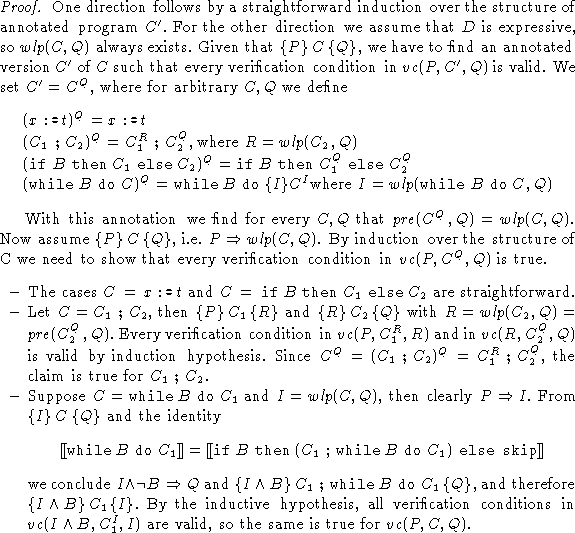
NPPV will prove many of these verification conditions by itself and list the remaining ones with the remark: ``Remains to prove : ''. The user will have to decide whether she accepts them as true, or whether she wants to store them in a log-file for later inspection.