C.A.R. Hoare has presented a calculus to derive theorems of the form 
,
where (P,Q) is a specification and C a program. There are two general logical
rules, an assignment axiom and one rule for every control construct .
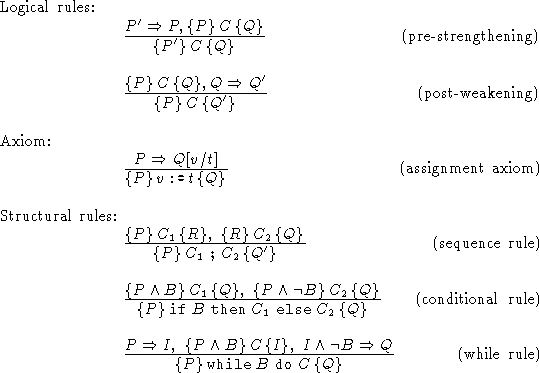
The rules can be formulated in several equivalent ways. Here they are
presented in a form that makes them appropriate for backward proof, that is, given a
program X, specification (U,V), to check that 
is true, proceed
according to the form of X and use the rules backwards: If X is a while loop,
use the while-rule, if X is an assignment, use the assignment rule, etc.
There are, unfortunately, several rules where a logical formula appears in the premise,
but not in the conclusion. In a backwards proof, this formula will have to be guessed.
This concerns the logical rules, the sequence-rule and the while-rule.
Fortunately it turns out that except for the while-rule, the unknown
expressions in the premises can be chosen in a standard way, as so called
weakest preconditions.
The logical expression I in the while-rule is called an invariant. There is no standard way to guess a proper invariant in a backwards proof, although a number of heuristics are available. We shall see later that finding a proper invariant is at least as hard as finding a proper induction hypothesis in an inductive proof.
The rules are easily seen to be correct. Since the premises contain predicate logic expressions that must be shown valid in the data structure, it is clear that logical completeness of the above set is out of the question. However, we can ask for relative completeness, that is completeness under the assumption of an oracle for the valid formulas of the data structure. It turns out that the rules are indeed relative complete in that sense, provided the data structure is expressive, a notion introduced below.