Objectives

• Further understanding of queue-based algorithms
• Introduction to simulation techniques

Introduction

We all know of many applications of queues in “real-world” situations. A prime example is the waiting lines. In order to improve customer service, techniques are sought to reduce the average waiting time, or the average length of the queue. For airlines companies, this could be to have waiting lines for regular customers, as well as waiting lines for the frequent flyers. For a supermarket, this would the use of express lines for customers with few items, as well as regular waiting lines.

However, in order to select the best strategy, e.g. adding 1, 2 or 3 express lines, managers need tools to estimate the value of certain parameters, such as the average waiting time, so as to implement cost effective solutions.

The are two main approaches to obtain these estimates. Queuing theory is a branch of mathematics that studies waiting lines. The alternative is to build computer simulations of these “real-world” systems, and measure the values of the parameters with help of the simulations.

For this laboratory, we are developing a computer simulation for a supermarket that has express and regular lines. These waiting lines will be implemented with help of queues.

The above figure shows the UML diagrams of the two main classes for the simulation. In addition to these classes, there is an interface, called Queue, as well as a simple implementation, called ArrayQueue. The source code can be found here:

• Queue.java
• ArrayQueue.java

As with most simulations, assumptions have to made to simplify the writing of computer programs.

• Our simulation is a discrete time simulation. It consists of a fixed number of steps. A clock is set 0 at the beginning of the simulation, which is then increased by a fixed amount (TICK) at each step of the simulation;
• At each step, one or more of the following events could occur:
  • A new customer arrives. The probability of a new arrival is PROBABILITY_NEW_ARRIVAL. The number of items purchased follows a uniform distribution, its interval is 1 …MAX_NUM_ITEMS;
  • A cashier processes exactly one item per step (assuming its associated waiting line is not empty);

The content of this laboratory has been adapted from Lambert and Osborne (2004) Java: A Framework for Program Design and Data Structures. Brooks/Coles, pages 266–274. You will find below the description of all the classes required for the simulation.

1 Customer

Write a class for modeling a customer. A customer knows its arrival time, its initial number of items, as well as the number of items remaining to be processed. The maximum number of items per customer is (MAX_NUM_ITEMS).

What are the instance variables? What are the class variables?

The constructor has a single parameter. It specifies the arrival time. The initial number of items is determined when the object is first created using the following formula:

Since, Math.random() generates a random number greater than or equal to 0.0 and less than 1.0, the expression MAX_NUM_ITEMS * Math.random() generates a number greater than or equals to 0.0 and less than MAX_NUM_ITEMS, adding 1 ensures that the number of items is greater than or equals to 1.0 but lower than MAX_NUM_ITEMS  1+. This real value is then converted to an int, in the range 1 to MAX_NUM_ITEMS , few! (here, I wanted to make sure that no customer would show up empty handed).

The instance methods of a customer include:

• int getArrivalTime() returns the arrival time;
• int getNumberOfItems() returns the number of items remaining to be processed;
• int getNumberOfServedItems() returns the number of items that have been processed;
• serve() decrements by one the number of items of this customer.

2 Cashier

A cashier is responsible for helping a queue of customers. It serves one customer at a time. Since the simulation is used to produce statistics, a cashier also memorizes the total number of customers served, the total amount of time the customers have been waiting, as well as the total number of items served (processed).

What are the instance variables? What are the class variables?

The class has a single constructor. It has no parameters. It initializes the instance variables of the cashier.

The method addCustomer( Customer c ) adds a customer to the rear of its queue. The method int getQueueSize() returns the number of customers currently waiting in line.

The method serveCustomers( int currentTime ) is a key element of the simulation. The method serveCustomers of each cashier is called once for each step of the simulation. The parameter currentTime is used to compute the total amount of time this customer has spent waiting in line. Here is the behaviour of the cashier when serving customers.

• If the cashier is not presently serving a customer, the next customer in line becomes the current customer, unless the queue is empty. Whenever, a customer is taken out of the queue, the cashier tallies the total amount time this customer spent waiting in line. If the cashier has no customer and the queue is empty, there is nothing to be done for this step;
• The cashier serves one item (a call to the method serve() of its current customer);
• If the current customer has no more items, the cashier adds the number of items of this customer to the tally. The state of this cashier object now indicates that this cashier has no current customer (the customer has been sent away).

There are also 3 instance methods used to report statistics for the total waiting time, total number of items served and total number of customers served by this cashier: int getTotalCustomerWaitTime(), int getTotalItemsServed(), and int getTotalCustomersServed(). Finally, the String toString() method returns a String that summarizes the statistics of this cashier.

Simulation

• Simulation.java

The class Simulation orchestrates the simulation. A Simulation object has two cashiers, one is responsible for the express line, the other for the regular line. The object also memorizes the duration of the simulation. The constructor the creates the two necessary cashier objects.

The method run() implements the main loop of the simulation. It sets the current time to zero then increments the current time by a fixed amount (TICK) at each iteration.

At each iteration, the method run must:

• Determines if a new customer has arrived, and if so place this customer in the appropriate waiting line (based on the number of items);
• Tells the two cashiers to serve their customers;
• Increments the current time.

At the end of the simulation, the method run() displays the statistics.

1. Execute the simulation several times. Discuss your observations with your neighbours. Here is an example of a run;
   SIMULATION ::  
   The duration (in seconds) of the simulation was 28800  
    
   EXPRESS LINE ::  
   The total number of customers served is 376  
   The average number of items per customer was 6  
   The average waiting time (in seconds) was 16  
    
   REGULAR LINE ::  
   The total number of customers served is 311  
   The average number of items per customer was 18  
   The average waiting time (in seconds) was 2597

2. As you can see, the average waiting time for the express line was short (16 seconds!) but the customers in the regular line are waiting nearly 45 minutes. The manager needs to add regular lines. But how many lines should be added? To answer this question, you will need to modify this application to allow for more regular lines;
3. If time allows, experiment with different parameter values: change the probability of an arrival, the number of items, the number of regular and express checkout lines.

3 Quiz (1 mark)

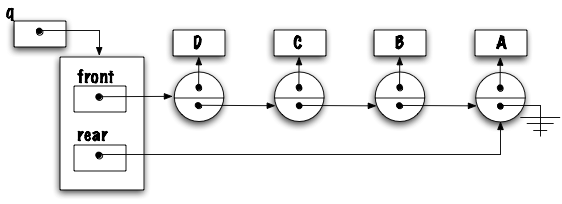
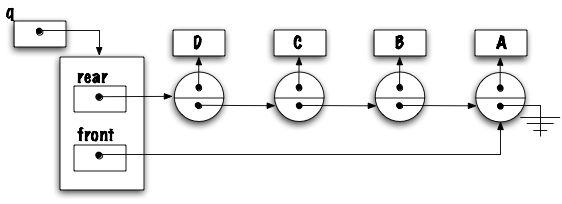
For the implementation of queue using linked elements, which of the following two implementations is preferable and why?

1. The instance variable front designates the first Elem object of the linked structure:

   

2. The instance variable rear designates the first Elem object of the linked structure:

   

• Write your answer to the above question directly in the text field of the submission Web page;
• http://uottawa.blackboard.com/

Last Modified: March 5, 2014