| Université d'Ottawa SEG-2106 : Software construction Gregor v. Bochmann Winter 2008, 2009, 2010, 2011, 2012, 2015 |
SEG-2106 - Lab 6 |
We consider the following non-deterministic automaton:
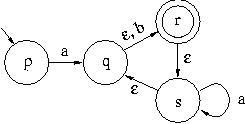
We consider the alphabet A={a,b} and the regular expression E=aa(a|b)*a
We consider the alphabet A={a,b} and the regular expression E=(a|b)*(abb|aaa) which defines the language of all words that terminate with abb or aaa.
We consider the following grammar:
E --> T | E - T | E + T
T --> SE | T * SE | T / SE
SE --> V | C | ( E )
V --> A | B
C --> 0 | 1 | 2 | 3
Write down a syntax tree for the following expression:
A + ( 2 + B ) / ( 2 * A )
Is the following grammar ambiguous ? - Explain in a few words why it is - or is not.
Grammar (A is the starting symbol) :
A --> a A c | a A | b
Prove that the following grammar is ambiguous:
S --> A B
A --> A id | id
B --> B id | id
id --> a | b | c
We consider the following grammar:
S --> S a B | A
A --> d A | c
B --> b | A
Which of the following sentences can be generated by this grammar ?
Write down a grammar for the language that consists of all strings formed from the characters a and b that have the same number of a as b. For example, the strings aabb, baba, and aabbababba are part of this language, but not the strings abb, bba, and aabbabb.
Explain why your grammar "does the job".
Write down a grammar that generates exactly all sentences of the following form: A sentence starts with an x which is followed by a certain number of y (at least 2); then there are a certain number of z (possibly zero) followed by one u and a certain number of v; finally there is another x at the end. The number of y must be equal to the number of v.
Explain why your grammar "does the job".
At the end of the Lab session, please show to the TA your draft texts and diagrams that you prepared for the work items (A) through (D). The TA will take note of the completeness of your work, but will not evaluate the quality of your work.
Please consult with the TA during the Lab session. The role of the TA is to help you to do the work suggested within this Lab.