State-Transition modeling - an introduction to different modeling paradigms

Transition: From the current state to another state, the next state (or destination state)

UML parlance: An event triggers a state transition. An action may be associated with a transition or with a state (do-action).

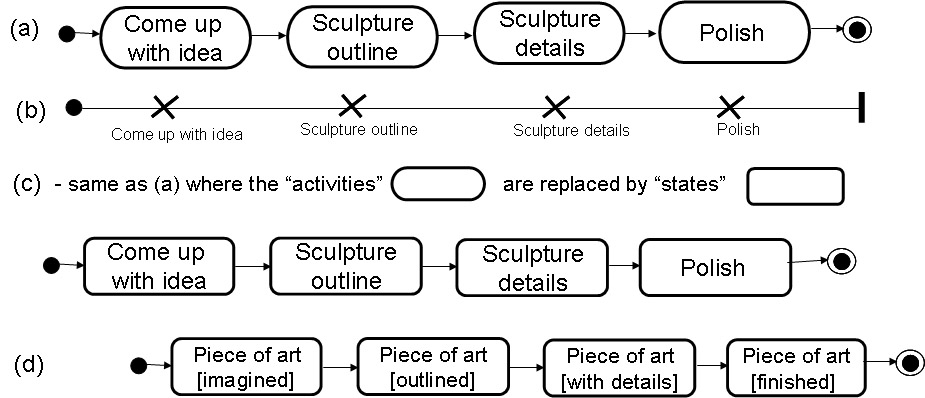
UML State vs Activity diagram: Example (from SEG-2106 course notes)

As an example, we consider the process by which an artist creates a wood sculpture (I remember, I did this when I was young): (1) the artist comes up with an idea of a sculpture, (2) s/he takes a piece of wood and prepares an outline of the sculpture, (3) the sculpture is refined in detail, and finally, (4) the sculpture is polished (and can be admired). Here are several representations of this process: (a) a UML Activity diagram, (b) a Use Case Map (UCM), (c) a UML State diagram representing the states of the artist working on the project, and (d) a UML State diagram representing the states of the sculpture. Note that diagrams (a), (b) and (c) have exactly the same meaning, while diagram (d) shows the process from another perspective, namely from the point of view of the object that is manipulated. In diagrams (a) through (c), the transitions between the activities/states are short, while some longer time periods are spent during the activities shown in the diagram (or the actions implied by the name of the states - in diagram (c)). In the perspective of the manipulated object (diagram (d)), the transitions take some longer time, while the states represent milestones - identifyable states of the object during the creating process. I would say that the diagrams (a) through (c) are action-oriented models, while diagram (d) is state-oriented. If we compare diagrams (c) and (d), we see that actions become states and states become actions. It is important to note that these two approaches can be used for describing the same reality. Which of these two approaches is better depends on the purpose of modeling.

In other words:

• Diagram (a) is a UML Activity Diagram. Each oval represents an activity, that is, an action. When an action has terminated, the arrow (a "transition") indicates what activity can be next executed. Such a transition is called (in UML) a completion transition - it is executed when the preceeding action is completed.
• Diagram (b) is a Use Case Map. It has the same meaning. A cross represents an activity, which is called "responsibility" in Use Case Maps.
• Diagram (c) is a UML State Diagram. Each rounded rectangular represents a state. In this example, each state represents an activity that is performed by somebody while the system is in that given state. So, this is an example of an "action-oriented" state machine model - each state represents an action, and the arrows represent transition from one action to another - again, these transitions a completion transitions.
• Diagram (d) is also a UML State Diagram. But it is "state-oriented" - each state shown actually represents the state of some object. The object here is the piece of art. The transitions between the states represent some actions that are performed to reach the next state in question. The tranitions here are not completion transitions (except the last leading to the final state) - they represent an action.
  • I think that "state orientation" is the normal way of using state machine models.

The same reality can also be represented by the UML Activity diagram below including object (data) flow. This diagram includes both views, the action-oriented and the state-oriented one. Here the data objects (represented by the rectangulars) represent the sculpture in its different states. Note: Here the transitions are associated with data objects that are produced by one action and consumed by the next action - they are actually inputs and outputs for these actions, namely the activities in the diagram.

Formal state-transition modeling:

1. State is something that does not change - a given situation - therefore we ignore the possibility of do-actions.
2. A transition from state s1 to state s2 is possible when the system is in state s1.
   • if we want to model triggering, we decompose the state s1 into substates, one where no trigger is present (and the transition is not possible - e.g. an event is at the head of an event queue), and one where the trigger is present (and the transition is possible).
3. Non-determinism: if there are two transitions from s1 (to s2 and to s3), then it is not determined which transition will be executed.
4. Basic liveness: If a transition is possible, it will be executed eventually.

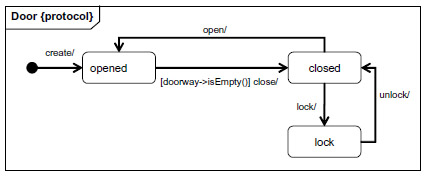
Labelled transition system (LTS): Has a finite number of states; transitions are labelled by actions names. Example: Door that locks

Rendezvous communication: Different LTS communicate by doing respective transitions with the same label simultaneously (only if both LTS are in a state where a transition with that label is possible).

Sometimes one distinguishes input (?) and output (!) labels - an output transition, say !out1, of one component is performed simultaneously with corresponding input transitions ?out1 of one or several other components - in this case, the LTS is sometimes called Input-Output Automaton (IOA). - Semantics of input-output: A component may take the initiative for performing an output transitions, but not for an input transition; the latter has to wait until it can make a rendezvous with a corresponding output transition of another system component. Example: The user of the door and the door do the above transitions in rendezvous - at the same time - and the user cannot perform the lock transition when the door is in the opened state. In this case the user actions may be considered output and the labels of the door as inputs.

Communication by interactions - Different kinds of interactions:

• Rendevous : synchronous (all parties involved perform a transition at the same time) - only if all parties are ready for the interaction - not clear which party initiates the interaction - possibly data transfer in all directions
• Procedure call : synchronous (only two parties) - initiating party is known - data transfer in both directions
• Input-output interaction - synchronous (all parties involved perform a transition at the same time) : one initiating party is known (for which the interaction is output) - for all others, the interaction is input - data transfer in one direction
• Input-output interaction - asynchronous (there are two sub-interations: (a) initation (sending a message), and (b) receiving the message (at a later time)

Interleaving semantics vs concurrency:

• interleaving semantics : only one interaction at any given time; transitions relating to different transitions are interleaved in time. This is what we assume normally in this course.
• concurrent interactions of different components : the related transitions occur at the same time, in parallel. This is common practice in the context of clocked hardware systems; one often considers synchronous FSMs of Moore type (all components perform a transition at the same time, synchronously).

Communication by variables - Finite State Machine (FSM) of type Moore: Has input and output - output can be modelled by variables. Value of output depends on state; the value of input may determine which transition will be executed - transitions may have input conditions. Example of Door that locks - modelled as two state machines that communicate by two input-output variables V1 and V2:

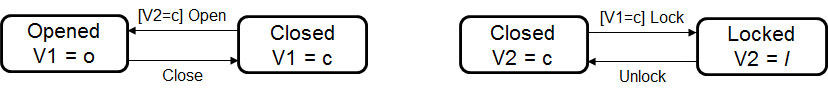
Another example that has the same behavior pattern - only the (informal) meaning of actions associated with the transitions of the second FSM are different: This example represents two doors that cannot be opened simultaneously. Note: The names of the states has no formal meaning (therefore only shown in grey) - but it may be helpful for human understanding.

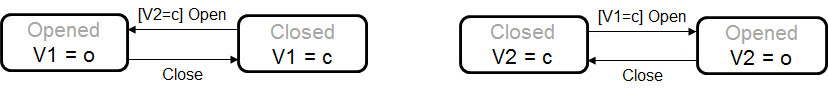
Petri nets: Generalization of LTS - transition may require tokens from more than one state - and may produce tokens for more than one destination state. In some sense, each token represents a point of execution, but their number is not fixed.

• Notation: transition is represented by a bar.
• Note: If there is always only one token in the net, this is equivalent to an LTS, where the token indicates in which state the LTS is.
• In general, there may be more than one token in a given state symbol of a Petri net (also called place).
• Note: The state of a Petri net is characterized by the distribution of tokens over the places (how many tokens are in each place).
• Example: Two doors that cannot be opened simultaneously. Note: The token distribution in the following diagram represent the initial state of this Petri net.

Finite State Machine (FSM) - Mealy type: Like Moor machines, except that inputs and outputs are messages (also called events, signals). Usually, one considers that the messages will be in transit (modelled as a message queue) before they are consumed as input by the destination FSM. Such a system is usually called Communicating FSMs. If there is no queuing of message, but messages are received as soon as they are produced, then this is equivalent to the IOA modeling paradigm.

Created: September 9, 2015