The meaning of behavior specifications (semantics) - comparisons

Need for semantics: Comparing specifications expressed in different formalisms

Often different behavior definitions for a given system component are given different description formalisms. For instance, the behavior of a method (declared in the interface of a given object class) can be desribed by the algorithm of its body - or by input and output assertions concerning its parameters and the values of the state variables of the object instance. Or the behavior of an accepting state machine, may also be defined by a regular expression. Often one of these behavior definitions appear to be more abstract than the other.

How can one compare such different specifications in order to determine whether they define the same behavior, or whether the behavior defined by one satisfies the requirements specified by the other ?

Answer: One needs a common model for the meaning of such specifications. The term semantics means meaning. What is the meaning of a behavior specification ?

Semantic model for safety properties

Trace semantics: The semantics of a behavior specification is the set of possible finite execution sequences. - Note: One often considers the tree of all possible sequences (see example in the Temporal Logic section above). Note: The set of specified sequences are those sequences that represent valid behavior of the specified system. Other sequences are not valid execution sequences.

Prefix-closure: One normally considers only sets of sequences that are closed under prefixing, that is, if a sequence σ is in the set then all its prefixes are also in the set, including the empty sequence.

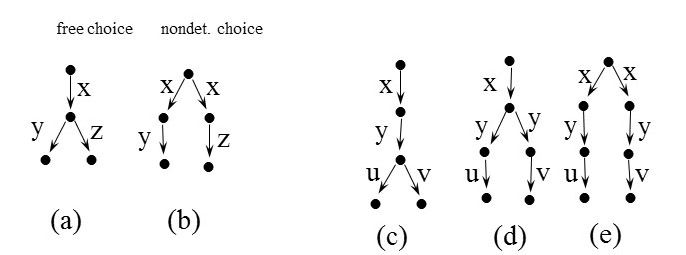
There are two views:

• State-oriented view: One considers the sequence of states that are reached during a possible execution of the specified system. This is normally the view taken with Temporal Logic (as explained above).
• Interaction-oriented view: One considers the sequence of interactions that are performed by the system during a possible execution. This is the view that is taken by specifications in the form of regular expressions, for instance

LTS specifications and other state machine specifications can be used with both of these views.

Deterministic specification: A specification S is deterministic if after any given valid sequence of interactions, the system is in a unique state. If for a given sequence of interactions, the system may be in one of several different states, the specification is called non-deterministic - the state of the system after a given interaction sequence is not determined uniquely.

Note: This kind determinism is sometimes called state-determinism, because the reached state is determined. In case of state machines that produce output, there is the possibility that in a given state different outputs interactions may be initiated. This is sometimes called output-non-determinism. A (state-) deterministic system may present output-nondeterminism, a (state-) non-deterministic system as well.

Trace equivalence: Two specifications S1 ansd S2 are trace equivalent if the set of possible finite execution sequences is the same.

Trace inclusion: Specification S2 satisfies the safety requirements of specification S1 if the set of execution sequences of S2 are included in the set defined by S1.

Another popular state machine formalism are Accepting Automata. They are LTS with a subset of states that are accepting. An interaction sequence is valid (called accepted) if the execution of this interaction sequence leads to (or may lead to) a state that is accepting. Note: The set of valid execution sequences is not necessarily prefix-closed. (It is prefix-closed if all states of the automaton are accepting - as can be said for LTS).

Transforming a nondeterministic specification into an equivalent deterministic one: There is a well-known algorithm (see section on Deterministic and non-deterministic (accepting) automata in the course notes for SEG-2106 A - at the end) which constructs an equivalent deterministic automaton from a nondeterministic one, based on trace equivalence. Unfortunately, the number of states of the deterministic automaton may be exponentially larger than the number of states of the given nondeterministic automaton; this means the algorithm has exponential complexity, but in most practical cases, it gives reasonable results. Note: An accepting automaton is like an LTS, except that only a subset of all states are accepting (one should be in accepting state at the end of a valid execution sequence). In the case of LTS, all states are accepting, because one does not formally talk about "final" states.

Algorithm for checking trace inclusion: For checking whether the traces of LTS1 are included the traces of LTS2, one usually takes the following approach:

1. Construct a completed version LTS2' of LTS2, which is obtained from LTS2 by adding a state Fail, and introducing new transitions from any state s of LTS2 to the state Fail for all those labels for which state s has no transition in LTS2.
2. Build the reachable behavior of the composition of LTS1 with LTS2'.
3. If there is a reachable state of the form (s, Fail) for some state s of LTS1, then there is a trace of LTS1 that leads the LTS2' into the Fail state, that is, LTS2 does not have this trace. Note: One assumes here that LTS2 is deterministic.

Other comparison criteria

There are other approaches to comparing the dynamic behavior defined by different specifications. In addition to safeness, one is often interested in liveness or progress properties or the absense of deadlocks. Let us consider some examples:

1. Assuming trace semantics, let us consider a given sequence σ that is included in the set of valid sequences, but there is no valid sequence of the form σ.x for some interaction x. Then the state reached by σ is a state which does not allow any further interaction. This is either a final state that is desirable, or it may be an undesirable deadlock.
2. As above, but there is a valid sequence σ.x for some particular x. If the specification is deterministic, then there is a unique state that is reached after the execution of σ, and this state is not a deadlock since the interaction x is possible from this state.
3. As as above, but a non-deterministic specification. Now the specified system may reach different states when σ has been executed. In one of these state, the interaction x must be possible, but there may also be another state that could be reached which is a deadlock. If the latter state was reached by executing σ, then the system would block after σ. That is, σ may lead to a deadlock. One therefore has to distinguish between may and must.

It is important to note that trace semantics is not able to distinguish between may and must reach a deadlock (one only can talk about must lead a deadlock). In order to specify such may properties, the so-called failure semantics has been introduced.

Failure semantics: Trace semantics does not deal with progress, liveness, blocking. Therefore comparisons based on blocking experiments, so-called failures, have been proposed (see CCS by Milner and CSP by Hoare - initially proposed around 1980) in the context of non-deterministic LTS. A failure is characterized by a trace T and a set of interactions I; the system has a possible failure (T, I) if after executing T and now offering all interaction from I as possible next interaction, the system may block. This means that T led the system into a state that has no transition for accepting any interaction in I. If the system is non-deterministic, it could be that another execution of T leads the system into another state that would not block.

• Testing equivalence: If two systems have the same failures they are called testing-equivalent.
• Reduction of nondeterminism: A specification S2 is a reduction of a specification S1 if they are trace equivalent, but S2 has less failures than S1. This implies that S2 has less possible (may) deadlocks.

Bi-simulation: While trace and failure semantics are based on observations of the possible interactions of the specified system with its environment (without talking about the states of the system), other interesting comparisons of state transition specifications are based on comparing the state machine structure. The most important comparison approach is bi-simulation: Can each specification simulate the other one ?

• Bi-simulation equivalence:
  • Two LTS specifications LTS1 (with the set of states S1) and LTS2 (with the set of states S2) have a bi-simulation relation if there is a relation R over S1 x S2 such that for any (s1, s2) in R,
    • if s1 --a-> s1' (for any interaction a) then there exists a s2' with s2 --a-> s2' and (s2', s2') in R
    • similarly: if s2 --a-> s2' then there exists a s1' with s1 --a-> s1' and (s2', s2') in R
  • The two LTSs are bisimulation equivalent if there is a bi-simulation relation with (s1-initial, s2-initial) is included in R.

Note that bisimulation equivalence implies testing equivalence, and the latter implies trace equivalence (but not the other way round). Among the following exmples, we have

• (a) and (b) are trace equivalent, and so are (c), (d). But they are not testing equivalent. (d) and (e) are also trace equivalent, and testing equivalent.
• (a) and (b) are not testing equivalent, nor (c) and (d). (d) and (e) are testing equivalent, but not bisimulation equivalent.

Created: September 17, 2014, updated Sept. 23, 2015