Hiding certain interactions - Abstraction by "projection"

If a system is composed of several components, one is often interested in viewing the system as a black box, showing only the external interactions, but not the interactions between the components within the system. One says that the internal interactions should be hidden. In other cases, one may be interested only in the interactions at one particular interface of the specified system, ignoring the interactions at another interface (called projection onto the visible interface).

Such a black-box view of a composed system or a projection on a subset of the interfaces is an abstraction of the original (more detailed) specification. The abstract view can be obtained from the original view:

• Hiding interactions in an LTS model: The LTS representing the abstracted view is obtained from the original LTS by replacing the transition labels of the hidden interactions by the label "i" (or "tau" or ɛ - the empty interaction, representing the empty sequence) which means an internal transition that cannot be observed. Such a transition is a spontaneous transition, that is, it may be performed without any interaction with the environment - a spontaneous state change.
  • The resulting LTS is in general state-nondeterministic.
  • The determination algorithm discussed above can be used to obtain a trace-equivalent deterministic LTS.
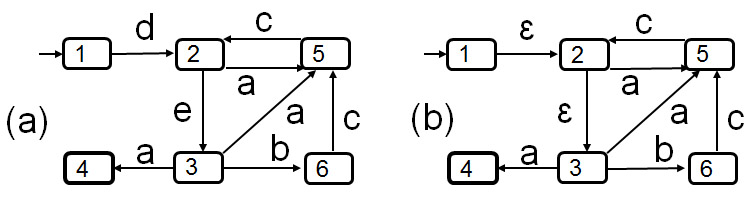
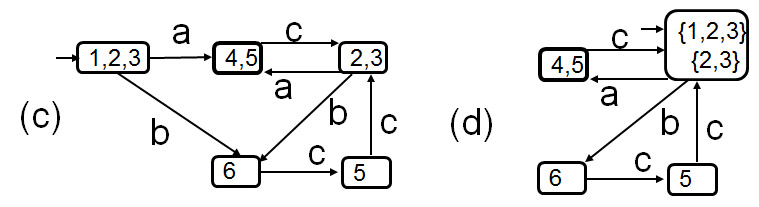
  • Example below: (a) shows an LTS with one accepting state 4. This LTS defines the same set of sequences of interactions as the regular expression d (a c)* e ((b c  +  a ) (c a)* c e)* a. (b) shows the same LTS with interactions d and e hidden - this is a nondeterministic LTS - when we replace in the above regular the interactions d and e by the empty string, we obtain the regular expression (a c)* ((b c  +  a ) (c a)* c )* a which is equivalent to ((b c  +  a ) c )* a. (c) shows a trace-equivalent deterministic LTS. (d) shows a trace-equivalent minimal LTS.
  • 
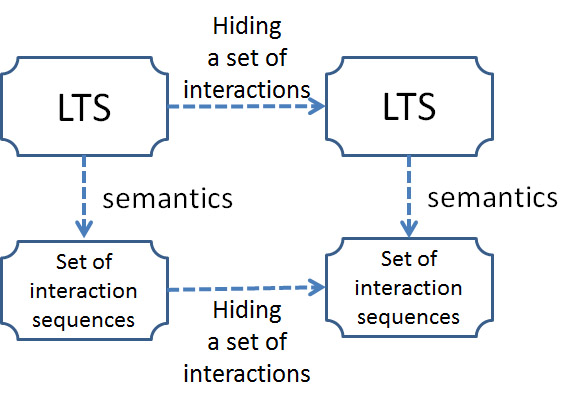
• Hiding interactions in execution sequences (semantics): The abstract view of a given interaction sequence σ is obtained by deleting in σ all interactions that are hidden (and leaving the other interactions in their original order).
• Can you prove that the following diagram commutes? - What does this mean ?
• 
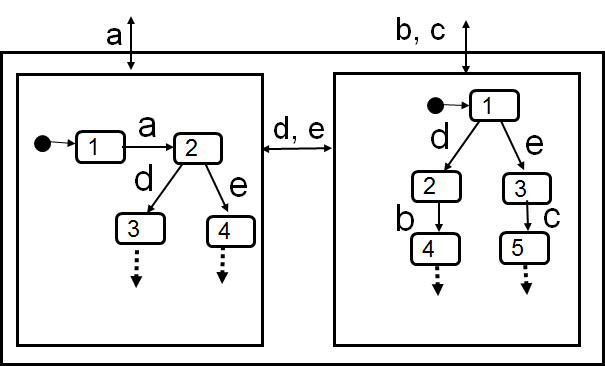
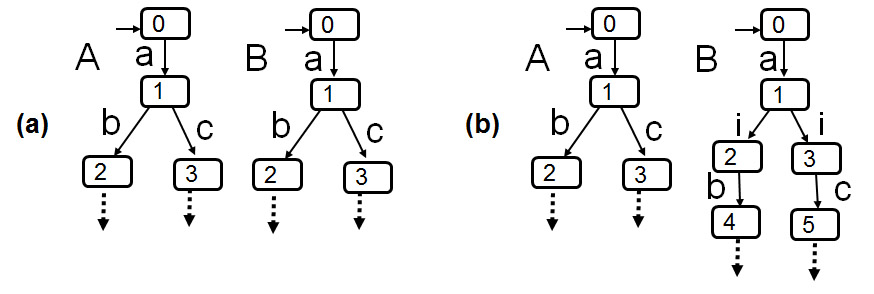
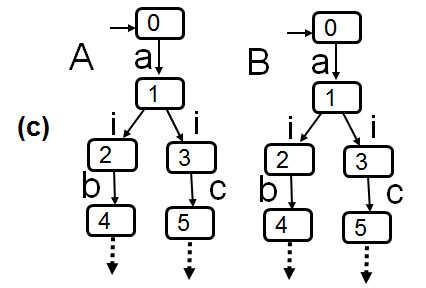
• Example: On the left: nondeterminism introduced by hiding. On the right: Which component makes the choice between interactions b and c ? - Possibility of deadlock.
• 
• 

An important example: Protocol verification

1. The service specification defines the requirements that the system containing the protocol entities and the underlying medium should satisfy.
2. The behavior of this system can be obtained by reachability analysis from the behavior of the two protocol entities and the medium.
3. The service specification takes a more abstract view by ignoring (hiding) the interactions between the protocol entities and the medium (the exchange of protocol messages). Therefore, before the behavior of the protocol system can be compared with the specified behavior of the service, we should hide the medium interactions from the detailed view of the protocol system behavior.
4. Then we obtain the abstract behavior of the protocol system which involves the same interactions as the service specification. We therefore can check whether these two specifications are equivalent, or whether at least all traces of the protocol system are included in the traces specified by the service (trace inclusion - to verify the safeness of the protocol).

Do this for a simple example, possibly using LTSA. See example CommProtocol-simple.lts (For the principle of safeness checking, see coffeeMachine - with tea safeness.lts )

See also the proof of the Alternating Bit Protocol (see my paper from 1978 - this is probably the first paper where it is shown how one can formally verify that a protocol specification gives rise to a given communication service)

Created: September 18, 2014