Temporal logic
In temporal logic, one considers assertions that hold on sequences of states that are reached during the execution of the system. Temporal logic is an extension of prediate logic which includes, in addition to the basic logic operations that apply to the properties of a given state, such as and, or, not, imply, also operators that relate to the sequences of future states over time. In the following, φ is a property that may hold for a given state. The temporal operators are the following:
- always φ (sometimes written Gφ, or □φ) means that the assertion φ is always true (from now on)
- eventually φ (sometimes written Fφ, or <>φ) means that the assertion φ will be true sometimes (now or in the future)
- next φ (sometimes written Xφ) means that the assertion φ will be true at the next time instance considered
- Q until P means that the assertion P is always true until Q becomes true, and also eventually Q holds now
Example LTS with state assertions A, B and C: 
- Initially, A holds. The transition diagram also implies the following temporal logic assertions.
- A implies next B (if we assume that each unit of time does one transition). Otherwise, we have Basic Liveness, which means that: if in the current state a transition is possible then one transition will be eventually executed. In this case we have:A implies <> B
- B implies <> (A or C)
- Initially: (A or B) until C - Note however: This only holds if we assume that the A-B loop will eventually terminate and C will become true (because this is part of the semantics of the until operator).
These operators can be used to express some other interesting time-related properties, such as
- □ <> φ - this implies that φ will be true infinitely often in the future
- <> □ φ - this means that starting some time in the future, φ will remain true
- □ <> x-is-possible implies <> x-was-last-operation-executed (this is called strong fairness for action x)
- <> □ x-is-possible implies <> x-was-last-operation-executed (this is called weak fairness for action x)
Example: Readers-Writers with an arbiter: 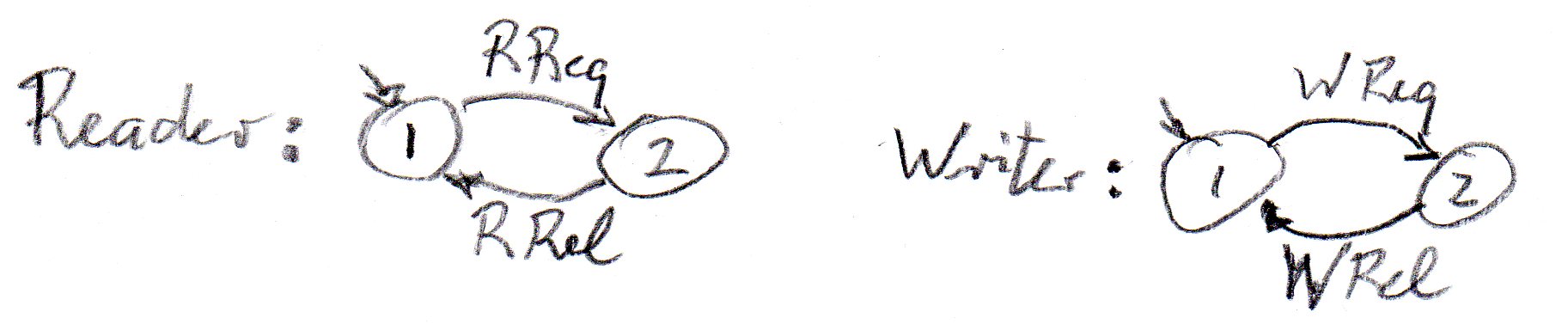
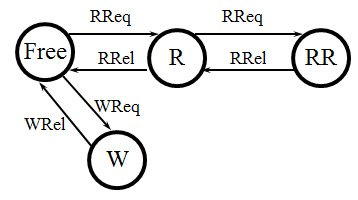
- The Reader wants weak fairness for the RReq operation in its initial state. This would be assured if the arbiter provides strong fairness for the RReq operation in its Free state.
- Would this assumption about the arbiter be sufficient to assure also weak fairness for the WReq operation of the Writer ?
- And what about the situation when there are two Readers ?
There are two types of temporal logics: Linear time (LTL) and branching time (CTL)
- In the case of linear time TL, the temporal logic property is valid on all execution paths - in each case, a sequence of discrete time instants is considered in the temporal order of that execution path.
- In the case of branching time TL, one distinguishes between properties that are valid for all execution paths and those for which there exists (at least) one path on which the property holds. One usually represents all these sequences by a tree.
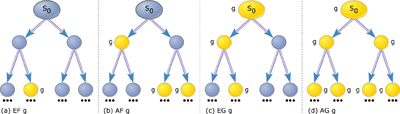
Table 1: Some temporal connectives in CTL
| EX φ |
true in current state if formula φ is true in at least one of the next states |
| EF φ |
true in current state if there exists some state in some path beginning in current state that satisfies the formula φ |
| EG φ |
true in current state if every state in some path beginning in current state satisfies the formula φ |
| AX φ |
true in current state if formula φ is true in every one of the next states |
| AF φ |
true in current state if there exists some state in every path beginning in current state that satisfies the formula φ |
| AG φ |
true in current state if every state in every path beginning in current state satisfies the formula φ |
Distinction of safeness and liveness properties - temporal logic - Büchi and Muller automata
A safeness property looks back in time. Such a property is described as follows: "Any finite execution sequence that is generated by the system will have such and such property" - for instance, conform with a given state transition diagram. On may say: "Whatever happens is good"
A liveness property looks forward in time. Such a property is normally described as follows: "If the system is in state X, eventually some property will hold", or "If the system enters state X infinitely often, then some state Y will also be entered infinitely often". On may say: "Something good will eventually happen"
In proving properties of programs, one considers so-called partial correctness (meaing that the results are correct if the program terminates), which is a safeness property, and termination, which is a liveness property.
The always operator of temporal logic is not really very interesting, since it describes safeness properties, as do state diagrams. The eventually operator is the interesting part of temporal logic because it allows to talk about liveness properties, such as eventual progress or termination, and fairness among choices.
Note that a liveness property can not be falsified by a finite execution history. Suppose the assertion <> P is to be checked on a finite sequence s, and P is false for all states encountered, this does not mean that <> P is not satisfied because P may become true at some later time. Eventually means it will be true at some time in the future, but we do not know when. Therefore a liveness assertion may be false only for infinite sequences - for instance, if <> P is false for all states of the infinite sequence. Therefore one considers normally infinite execution sequences when one talks about liveness.
There are alternative ways to talk about liveness properties for infinite execution sequences, using extension to state-transition diagrams - instead of temporal logic:
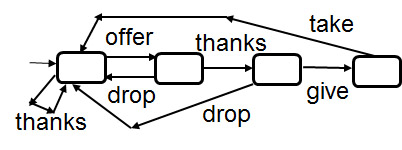
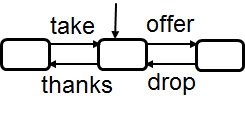
- Büchi automata: Certain states are annotated as accepting states - which means that for each valid infinite execution sequence, among all states that occur infinitely often within that sequence, there must be one state that is accepting. For instance, if in the Offer-Take example, Case-4, only the right-most state is accepting, then the smaller loops will always terminate and the big loop involving the take operation will be executed infinitely often.
- Muller automata: A certain number of subsets of states are identified as accepting subsets - which means that for each valid infinite execution sequence, the subset of states that occur infinitely often within that sequence must be one of the accepting subsets. For instance, in Case-5, if the automaton has one accepting subset which contains all three states, then the choice between the two alternatives is fair. This is more difficult to model with Büchi automata.
- Examples: Case-4 and Case-5
 - - -
- - - 
- Note: Another interesting modeling paradigm are Muller transition automata (I currently do work on this topic). In this case a subset of the "live" transitions must be executed infinitely often by an (infinite) execution sequence. For instance, if in the example Case-4, the transition drop is not included, then the small offer-drop loop will not be executed infinitely often. This cannot be expressed by a Muller automaton of the same shape, or a Büchi automaton of the same shape.
- If there is a state with several outgoing live transitions then the choice between these transitions must be fair (Reason: if a transition is treated unfairly, then it will not be executed infinitely often).
Created: September 2, 2014, updated Sept. 22, 2015


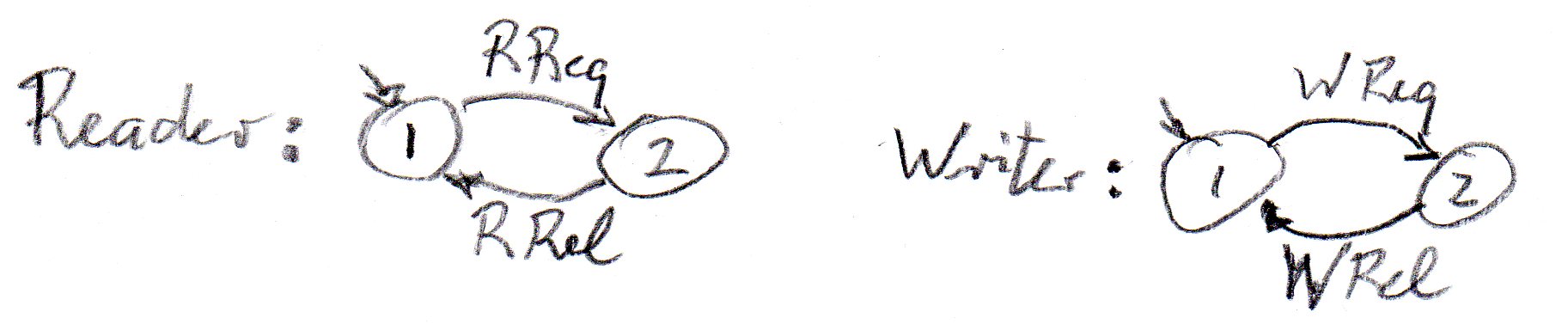


 - - -
- - - 