For simplicity, one often considers state-transition models with a finite number of states. Often this is too limiting and one uses so-called extended state-transition models where the state includes the value of state variables and interactions may include data parameters. One needs more powerful specification formalisms for defining their behavior.
In general, a transition system is a system that is characterized by (1) a set of states in which it could be, (2) a subset of these states which are the possible initial states of the system, and (3) a finite set of (possibly parameterized) transitions. Besides its name, a transition is characterized by a subset of states in which it is enabled and a transition function that identifies for each of these enabled states what the next state of the system is if this transition is executed. In the case of a non-deterministic transition system, the transition function may be multi-valued, that is, define a set of possible next states for each of the enabled starting states.
Example 1: Grocery store with initial capital of C_init dollars. The state space of the system is the set of all pairs of integer numbers, corresponding to the values of the variables C and G. There are two transition, named s and b. For each transition, the enabling condition indicates what the enabled states are, and the action indicates what the transition function is. This transition system is deterministic.
The grocery store (above) has an infinite state space (if one assumes that there is no limit about how rich a grocery store may become). C_init is a parameter of the grocery store instant. n is a parameter of the transition s. (We see that the cost of a goodie is fixed, and double the wholesale cost used by the b transition). Exercise: consider the possible states that can be reached by this system depending on the initial capital provided.
Here a different notation is used. The enabling condition of a transition is written to the left of the symbol "-->", while the action is writtten to the right. The action is written as a concurrent assignment statement, meaning that the assignments to the variables are done concurrently; for each variable, an expression is given that defines the next value of the variable. These concepts have been integrated in several high-level programming/specification languages, such as Dijkstra's "guarded commands" or the specification language Unity by Misra and Chandy.
First-order logic has often been proposed for writing specifications for dynamic systems. For instance, for the documentation of the behavior of a method call, one sometimes uses an pre-condition and an post-condition. The pre-condition defines the assumption that the system makes about the validity of a method call, depending on the current state of the system and the input parameters of the method call. The post-condition defines what the system implementation must guarantee about the values of the output returned and about the new state of the system after the method call (both in general depending on the method input parameters and the current state of the system).
In Example 2 above, the enabling condition of the put transition is a pre-condition, while the enabling condition for the get transition includes also the post-condition about the returned value (written in the form of an assignment statement). The actions for both transitions represent post-conditions for the transitions, defining the next state of the system. This kind of notation results in an executable model, since assignment statements of this form are easily executable.
One can use a more general form for writing the specification of a transition in first-order logic. Sometimes, one simply characterizes a transition by a single boolean expression which is the conjunction of the enabling predicate (which may be called the pre-condition) and the post-condition for the returned results and the next state of the system. In the post-condition, however, one may have to refer to the variable values before and after the execution of the transition. In order to distinguish these two values, the new value is normally denoted by the name of the variable followed by " ' " , for instance, the transition put of Example 2 may be characterized by the condition: size < N and size' = size + 1 . This notation is used, for instance, by Z and TLA.
The disadvantage of this more general notation is that the resulting specifications are in general not executable, because it is not decidable how to find a next value for the state variables (or a returned result value) that make the boolean expression of the transition become true.
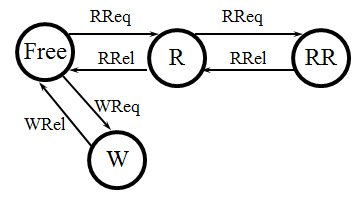
When the state space of the system is finite, the specification of the transitions can be written down by enumeration in the form of a state diagram, as shown by the following simple example.
Example 3: Shared read-write resource

This system has 4 possible states, and the following transitions: WReq (write request), RReq (read request), WRel (write release), and RRel (read release). For instance, the transition RRel is enabled in the states R and RR, and the next state is Free if the current state is R, and it is R if the current state is RR. Note: this is a model of a resource that can accept up to two concurrent readers, but not more.
Finite state transition modeling is often too restrictive, one needs transition parameters and state variables. Therefore one often uses so-called extended finite state transition models which combine the simplicity of the finite state transition modeling paradigm with the power of transition parameters and state variables as explained in first subsection on "Transition systems - in general" above. This is for instance done for UML State transition diagrams and many other formalisms.
The different state machine models discussed above (as well as Petri nets discussed later) are often extended to be able to model realistic situations in a more complete and/or more concise manner. Basically, these extensions are always the following:
Here is a simple example showing a shared read-write resource that does not have the restriction of only two concurrent readers.
Example 4: Shared read-write resource with an arbitrary number of concurrent readers
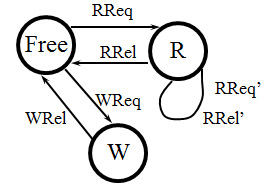 |
Besides distinguishing the three states of the diagram (which could be encoded as three possible values of a variable STATE, sometimes called the "major state"), this system has an additional state variable, called N, which represents the number of active readers. The transitions related to readers have the following enabling conditions and actions:
|
In the above example, the underlying finite transition system is an LTS. Similar extensions can be defined in a similar manner for other finite state transition models, such as FSM and IOA, as well as for Petri nets.
Created in 2007; updated: 2011, January 24, 2012, Sept. 2014