Introducing input-output into LTS

There are different ways of introducing the notion of input and output interactions into the formalism of LTS.

Role of interaction parameters

The LOTOS language (see http://en.wikipedia.org/wiki/Language_Of_Temporal_Ordering_Specification C ) uses rendezvous communication, where interactions may have parameters. Each participating component may impose constraints on the acceptable parameter values. As an example, we consider two processes A and B that communicate over a joint port called P by the joint interaction g (integer par) which has one parameter of integer type. We consider different cases:

1. Nondeterministic value creation: In this case of a simple rendezvous, a common value will be created nondeterministically
   • A: ... ; P.g(x); ...
   • B: ... ; P.g(y); ...
   • After the rendezvous, the local variables x and y will have the same value. Note that the rendezvous g(x) stands for a set of possible rendezvous g(v) for all values of v that are allowed according to the type definition of the parameter in the interaction declaration. Both parties, A and B must perform the same interaction in rendezvous, therefore using the same value for the parameter.
2. Value constraints: both parties may impose constraints on the values of interaction parameters
   • A: ... ; P.g(x) [x > 5]; ...
   • B: ... ; P.g(y) [y < 12]; ...
   • In this case the parameter during the rendezvous must be in the range from 6 to 11.
3. Value passing: one party has no contraint, the other imposes a particular value to the parameter
   • A: ... ; P.g(x) [x = expression]; ...
   • B: ... ; P.g(y) ; ...
   • In this case the value of the local variable y will be equal to the expression used by party A.

It is clear that in case 3, the parameter of the interaction g is output for component A and input for component B.

Informal distinction of input and output

The designer chooses names for the interactions that implicitly indicate whether the interaction is input or output.

• Difficulty: An interaction that is output for one component is input for the other component. The LTS convention of having rendezvous communication for interactions of different components with the same name makes this difficult. In the example of the CommProtocol-Simple this difficulty does not arise, since the communication is between one protocol entity and a communication queue - output for the entity (the name starts with an "s" for sending) implicitely is input for the queue - and the name selected corresponds to the view of the protocol entity.

Formal notation for distinguishing input and output for rendezvous communication

Because of the above difficulty, several people have introduced a formal notation for distinguishing input and output, but retaining the communication primitive of rendezvous, that is, the input and output operations are performed by the participating components as a single, atomic action. Examples of such notations are the following:

• underline notation of [Bochmann 1978]. Rendezvous communication for interactions with the same name - the output action is identified by underlining.
• overline notation of CCS [Milner 1980]. Similarly.
• The "!" - "?" notation: An output (inptu) interaction is identified by the character "!" ("?") before or after the interaction name. This has become a widely used convention, for instance, also used by the UPPAAL tool.

Important note: Here it is assumed that interactions are always rendezvous, that is, both parties must be ready to participate in the rendezvous.

Considering interactions as events

In UML, the concept of an events is widely used. An event is an action that happens. It is usually triggered by some process, and handled by another process (that is, the latter performs some processing that is appropriate for taking this event into account). In a typical state machine defined in UML, an input to a state machine is an event (it is initiated by some process in the environment of the machine), and the machine will handle the event by performing a corresponding state transition (defined by the state machine model).

Based on this semantics of interactions, one can say that for each interaction:

• There is one component that initiates this interaction. The interaction is output for that component.
• For all other components participating in that interaction, the interaction is input. The input is processed by performing some state transition.
• If the interaction has parameters, the value of these parameters are determined by the outputting component, and the other component may use this value during the processing of the input interaction.

It is important to note that the question whether an output will be produced by the outputting component is solely determined by that component, and not by the component that receive that output as input.

There are two underlying semantic models:

• Direct coupling [Bochmann 78]: The input processing is done immediately when the output is produced by the outputting component - as a single atomic interaction. This is also the semantic model for so-called Input-Output Automata (IOA). - This is what we assume in the following in this chapter.
• Message queuing: The event of producing an output (in the form of a message) is a separate action from the handling of the message as input by the other components. After production, the output is first placed in the input queue of the corresponding inputting components. This semantic model is often called Communicating Finite State Machine (CFSM, see next chapter of this course).

Completely defined state machines

Definition: A state machine, e.g. LTS, is completely defined if in each state there is a transition for all transition labels that are part of the alphabet of the state machine. Otherwise, it is called a partially defined state machine.

A completely defined machine accepts in each of its states, all interactions. An LTS is normally not completely defined. Two completely defined LTS will never deadlock when they communicate.

Definition: An IOA or a CFSM is completely defined if in each state there is a transition for eqch inputs in the input alphabet of the machine.

IOAs are often considered to be completely defined, however, this represents in many case an overspecification. In hardware design one talks about don't care condition for the output of a component for certain input values. It means, it does not matter what the output would be - the output is not specified for those input values.

In component-based system development, one knows normally what kind of components are used in the environment of a given system component. Therefore the behavior of the environment is known, and it can be predicted that certain inputs to the given component will not be produced by the envirnment when the given system is in certain states. Therefore it would be an overspecification if one would define the required state transitions for handling such inputs in those states.

This leads one to consider that the specification of a components includes assumptions about the environment and guarantees about the (output) behavior of the given component (but only for the case that the environment follows these assumptions). See specification with assumptions and guarantees.

Specifying assumptions and guarantees with partially defined input-output state machines

Semantic model for partially defined input-output state machines: The states and transitions specified in the model define the guarantees about the behavior of the component that is specified. For each state of the model, it is assumed that the inputs for which there is no transition defined from this state will not occur during the execution of the system where the component is used. In case that such an input occurs in some exceptional situation, the behavior of the specified component is not defined - it may react arbitrarily, possibly going to a blocked state.

Verification of component-based designs: With this semantic model, when a component-based system is designed, it is important to verify that the assumptions made for each component are satisfied by the behavior of the components in its environment.

• In the case of LTS modeling, the most important design problem that occurs in component-based systems is deadlock (see earlier).
• With assumption-guarantee specification, we have in addition the possible design problem, that a component receives in input for which is does not have a transition in its current state. This condition is called an unspecified reception (first described by C. West in the late 1970ies when he designed a tool for avoiding such design faults)

Verification algorithm: Similar to the Algorithm for checking trace inclusion, one completes the specification of the component behaviors by introducing a state Fail for each component, and then one performs reachability analysis. If any of the reachable states includes the Fail state of any of the involved components, there is a unspecified-reception design fault.

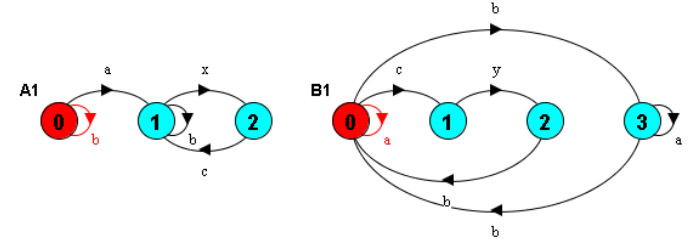
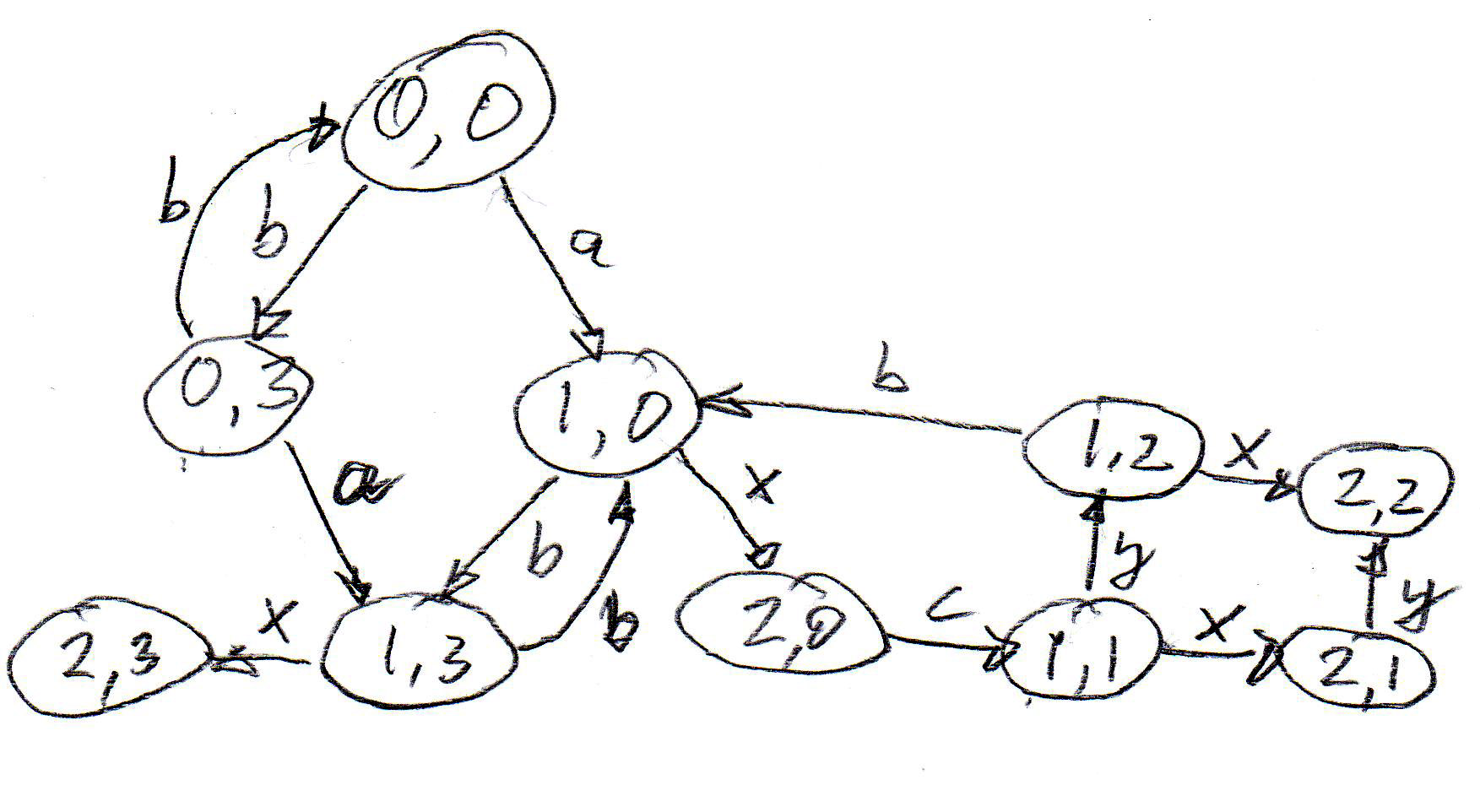
Example (the same as used for LTS reachability): Which interactions are input/output for A1 and A2 ? - To be selected, and reachability analysis to be adapted.

Reachability analysis considering the possibility of unspecified reception

Reachability analysis for IOA is in some sense similar as for LTS. Here transitions are labelled !m (output of the message m) or ?m (input of the message m). Transitions that have labels containing the same message are performed jointly.

However, there is one very important difference: Whether an output transition is performed is decided by the outputting component alone. If the component that should receive the message is in a state where it does not have an input transition for this message, one encounters a non-specified reception situation (which can be interpreted in different ways - see discussion). Note that similar situations for interacting LTS sometimes represent deadlocks (no transition is possible for the global system).

If Ii is the set of input messages of a component Ci, and Oi is the set of its output messages, we assume that Ii intersection Oi is empty and we define the alphabet Ai = Ii union Oi. In a composition, a given message may be output only for one component; but it may be input to several components (for instance, it may be output generated by the environment and be input to several components). We assume here that all messages between two components are also visible to the environment; this means that an interaction that is output by one component is also an output from the composition to the environment. Note: A hiding operation for the inter-component messages may be performed after the reachability analysis.

The composition of two IOA models, C1 and C2, with alphabets A1 = I1 union O1, and A2 = I2 union O2, respectively, can be modeled by a global IOA that represents the behavior of these two component IOA and their interactions, in the following called C. The model of C is the following IOA (Note: rules (1) and (2) are the same as for LTS):

1. The states of C are of the form <s1, s2>, where s1 is a state of C1 and s2 is a state of C2.
2. The initial state of C is the set of states <s1-initial, s2-initial> where si-initial are initial states of Ci (i = 1, 2).
3. The transitions of C from a state <s1, s2> are the following:
   • for m in O1 and in I2
     • if there are transitions s1 -- !m --> s1' in C1 and s2 -- ?m --> s2' in C2 : then <s1, s2> -- !m --> <s1', s2'> (input and output transitions executed jointly; this is output to the environment)
     • if there is a transition s1 -- !m --> s1' in C1, but no transition s2 -- ?m --> to any state in C2 : non-specified reception (design error)
     • if there is no transition s1 -- !m --> to any state in C1, but there is the transition s2 -- ?m --> s2' in C2 : no transition in the composition (maybe the transition of C2 will never be executed - this depends on the other states of C1 that may occur jointly with s2)
   • for m in A1 and m not in A2 (C2 is not involved in this interaction - direct interaction between C1 with the environment)
     • if there is a transition s1 -- m --> s1' : then <s1, s2> -- m --> <s1', s2> (transition by C1 alone)
   • similarly as above, for C1 and C2 interchanged
   • for m in I1 and in I2
     • if there are transitions s1 -- ?m --> s1' in C1 and s2 -- ?m --> s2' in C2 : then <s1, s2> -- ?m --> <s1', s2'> (joint transition when input m comes from environment)
     • if there is a transition s1 -- ?i --> s1' in C1 , but no transition s2 -- ?i --> to any state in C2 : possibly a design error, but this depends on the behavior of the environment (non-specified reception for C2 if input comes from environment when C2 is in this state); otherwise the transition of C1 will never be executed. Similarly, for C1 and C2 interchanged.
   • for m in O1 and in O2 : this is not allowed according to what is said above - miss-match of the interfaces between the two components - conflicting output transitions

Created: September 22, 2014